1

For a given directed acyclic graph G with only known successors I am trying to find all direct and indirect predecessors and successors for any possible given node N. The ordering of the solution should be precedence feasible and the solution should contain N itself. A resource-saving solution would be nice since the size of G may increase drastically.

Example:

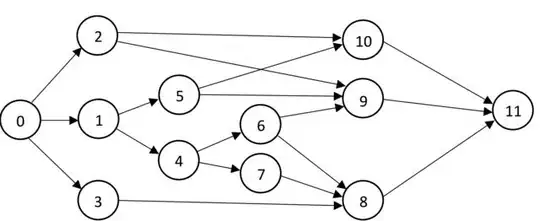
enter image description here

G = {0: [1,2,3], 1: [4,5], 2: [9,10], 3: [8], 4: [6,7], 5: [9,10], 6: [8,9], 7: [8], 8: [11], 9: [11], 10: [11], 11: []}

For N = 8

[0, 3, 1, 4, 6, 7, 8, 11]

or 

[0, 1, 4, 7, 6, 3, 8, 11]

would be precedence feasible solutions, but not

[0, 3, 1, 6, 4, 7, 8, 11]

since 6 is a successor of 4.

As shown above there is the possibility that several solutions exist. One would be sufficient but it would be nice if it is not always the same for a given N (if multiple solutions exist).

qualitaetsmuell
  • 141
  • 9

1 Answers1

0

Here's a summary of the solution:

  1. For a given starting, and ending point, and for specific value N, list all possible paths that pass through N.
  2. Compute the length for all path combinations (direct and indirect), and create a dictionary, where key is the length, n, and the value, are indexes of the paths.
  3. Merge the paths for given N, while maintaining precedence feasible solution

Details

Step 1

To list all the paths for a graph, I am using this solution here, with some modifications: 

 G = {
    0: [1,2,3], 
    1: [4,5], 
    2: [9,10],
    3: [8],
    4: [6,7],
    5: [9,10],
    6: [8,9],
    7: [8],
    8: [11],
    9: [11],
    10: [11],
    11: [],
    }

G2 = {k:set(v) for k,v in G.items()}

def dfs_paths(graph, start, goal):
    stack = [(start, [start])]
    while stack:
        (vertex, path) = stack.pop()
        for next in graph[vertex] - set(path):
            if next == goal:
                yield path + [next]
            else:
                stack.append((next, path + [next]))

def run_paths(graph, start, end, N = None):
    all_paths = dfs_paths(graph, start, end)
    if N == None : 
        return([x for x in all_paths])
    else:
        return([x for x in all_paths if (N in x)])

Notice in run_paths(...), if N is specified, the function will return the paths that only include N.

print(run_paths(G2, 0,11))
[[0, 3, 8, 11], [0, 2, 10, 11], [0, 2, 9, 11], [0, 1, 5, 10, 11], [0, 1, 5, 9, 11], [0, 1, 4, 7, 8, 11], 

print(run_paths(G2, 0,11, 8))
[[0, 3, 8, 11], [0, 1, 4, 7, 8, 11], [0, 1, 4, 6, 8, 11]]

Step 2

Using the pairwise function described in itertool documentation, we can generate all paths combination indexes and compute their paths. The set() function will eliminate duplication when counting for direct and indirect paths. Finally, create a dictionary where the key is the length of the array and the value are list of the associated paths indexes. 

from itertools import *
def get_size_dict( list_of_sols ):
    def powerset(iterable):
        s = list(iterable)
        return chain.from_iterable(combinations(s, r) for r in range(len(s)+1))

    comb_of_indexs = powerset(range(len(list_of_sols))) # return a comb of indicies
    d = {}
    for indexs in comb_of_indexs:

        myset = set([x for index in indexs for x in list_of_sols[index]])
        set_length = len(myset)
        if set_length not in d.keys():
            d[set_length] = []

        d[set_length].append(indexs)

    return(d)

For our example, the function will return, the following dictionary, given the output from step 1. 

{0: [()], 4: [(0,)], 6: [(1,), (2,)], 7: [(0, 1), (0, 2), (1, 2)], 8: [(0, 1, 2)]}

and if we needed N = 8, we need to use path index 0, i.e. [0, 3, 8, 11], index 1 and index 2.

Step 3

Merging the paths. The technique used here is to identify where the common nodes between two paths. Then looping over each pair of the common nodes, find the nodes between them in the first path and append it to a list then do the same for the 2nd path. Then we can use the reduce function to apply this technique to merge multiple paths.

from functools import *

def merge_paths(a, b):
    def pairwise(iterable):
        "s -> (s0,s1), (s1,s2), (s2, s3), ..."
        a, b = tee(iterable)
        next(b, None)
        return zip(a, b)

    def find_elements(x, text1, text2):
        return(x[x.index(text1)+1:x.index(text2)])

    my_list = []
    interesect_points = [x for x in a if x in b]
    for (x,y) in pairwise(interesect_points):
        ''' 
        get elements from a that within x,y --> e1
        get elements from b that within x,y --> e2
        if my_list is empty:
            add x,e1, e2, y to my_list
        else add e1, e2, y
        '''
        e1 = find_elements(a, x, y)

        e2 = find_elements(b, x, y)

        if len(my_list ) == 0:
            my_list.extend([x] + e1 + e2 + [y])
        else:
            my_list.extend(e1 + e2 + [y])

    return(my_list)

Completing the Solution

The final part, the function process_graph that wraps all the functionality discussed earlier.

Once we compute the lengths in the dictionary d, if the value N is not part of the dictionary's keys, the function terminates and returns None.

def set_for_size_N(paths, indexes ):

    for index in indexes:
        yield [paths[i] for i in index]

def process_graph(G, start, end, N):
    paths = run_paths(G2, start, end, N)

    d = get_size_dict(paths)
    if N not in d.keys():
        return(None)

    list_of_paths_of_size_N = set_for_size_N(paths,d[N])
    for paths_of_size_N in list_of_paths_of_size_N:
        yield(reduce(merge_paths, paths_of_size_N))

The output for N=8: 

for i in process_graph(G2, 0, 11, 8):
    print(i)
[0, 3, 1, 4, 7, 6, 8, 11]

And here's another example for N=6:

for i in process_graph(G2, 0, 11, 6):
    print(i)
[0, 1, 4, 6, 9, 11]
[0, 1, 4, 6, 8, 11]

This may not be the most efficient or delicate solution, and there is room for improvement.

see-king_of_knowledge
  • 523
  • 3
  • 6