Recursions of the form T(n) = T(n - n^(1/q))

Question

I am trying to find an answer to the following problem:

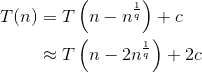
T(n) = T(n - n^(1/q)), q > 2
T(c) = O(1), for a constant c

What I am interested in are recursive problems, which do not branch and do not have any auxiliary calculations. Something similar to this problem. The difference is that the amount by which my problem is going to be reduced also gets smaller in each recursive call. I've tried to solve this via an iterative approach leading to this:

T(n) = T(n - n^(1/q) = 
     = T[n - n^(1/q) - [n - n^(1/q)]^(1/q)] = 
     = ....

for which I cannot really find a reasonable expansion. I therefor tried the substitution method for T(n) \in O(n) and T(n) \in O(log(n)), which both hold, if I haven't made any mistake.

Given that I can now only assume that T(n) = T(n - n^(1/q)) \in O(log(n)), for q > 2, which seems reasonable, since it is very similar to binary search.

Sadly I haven't really covered such recursions, neither do I have a good idea of applications following such recursions.

Given all of that my questions are:

Can we reason about recursive problems which do not branch and do not have auxiliary calculations comparable to the statement above?

Are there applications of algorithms which have such a behaviour? I guess it could appear when searching in a linear field, very similar to binary search, but not with cutting the field in halves?

Similar problems are the following: T(n) = x + T(n-log(n)) and T(n) = T(n^(1/2)) + T(n-n^(1/2)) + n

Edit: Removed wrong expansion.

T(n) = T(c). if this is a real problem, you probably need to add a constant cost somewhere. — Matt Timmermans, Nov 17 '19 at 23:46
The expansion step you tried, `(n - n^(1/q))^(1/q) -> n^(1/q) - n^(1/q^2)`, is incorrect. Instead you should perform a *binomial expansion*, after which you'll find that every term, *apart from* the one proportional to `n^(1/q)`, will be very small at large values of `n`. — meowgoesthedog, Nov 18 '19 at 17:23
@MattTimmermans Thanks, it occurred to me that that seems to be more reasonable, that you have to add some constant auxiliary terms. — spranger, Nov 18 '19 at 18:04
@meowgoesthedog Thanks, yes. That is not correct. Although it shouldn't change anything regarding the topic, since I didn't finish it anyways... — spranger, Nov 18 '19 at 18:05

meowgoesthedog · Answer 1 · 2019-11-19T11:18:49.690

Perform a binomial expansion on the second term:

This can be done because 1/q < 1, which in turn means n^(1/q-1) << 1 for large values of n.

Substitute back into the recurrence:

1 - 2/q > 0 because q > 2, so the third term quickly decays for large values of n, which means it can be ignored in the asymptotic limit:

Using a similar technique, the next expansions would be:

Therefore:

Some numerical test results:

q   | 3       4         5         6         7         8         9         10
m   |                                 T(10^m, q)
------------------------------------------------------------------------------------
1   | 8       10        10        10        10        10        10        10
2   | 38      54        65        81        100       100       100       100
3   | 164     272       389       486       563       627       755       1000
4   | 728     1447      2222      2994      3761      4554      5255      5511
5   | 3300    7835      13471     19497     25699     31681     36869     43686
6   | 15149   43199     82438     128804    177495    226212    275381    343686
7   | 69946   240337    511496    854128    1249628   1648028   2123037   2586014
8   | 323861  1343497   3193858   5735972   8792779   12228031  15705474  19268220
9   | 1501499 7529750   20024691  38712540  62366319  89586305  120308456 152184297
10  | 6965614 42264115  125845996 262058267 444972781 664753359 914166923 1188039787

Log-log plot of T(n) against n, for all values of q:

Linear log-log plots correspond to polynomial relationships, which agrees with the theoretical result of n^(1-1/q). The exponents are given by the values of the gradients:

q   1-1/q       gradient
---------------------------
3   0.666666667 0.658929415
4   0.75        0.736456264
5   0.8         0.786448328
6   0.833333333 0.818586522
7   0.857142857 0.841039047
8   0.875       0.860906137
9   0.888888889 0.875722729
10  0.9         0.886571495

The gradients match the theoretical values reasonably well, but are on the low side. This may have been due to integer truncation in the code used for numerical tests.

Recursions of the form T(n) = T(n - n^(1/q))

1 Answers1