There are different algorithms used to find the nodes such that if removed they make the graph disconnected (called articulation points).
Here I explain one of them and I provide some code that implements it:
Tarjan Algorithm
Given a graph 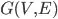 we want to find all the
we want to find all the 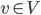 such that if
such that if 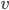 is removed from
is removed from 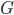 the graph become disconnected
the graph become disconnected
The first observation is that the a (weak) connected component in a directed graph is equal to a connected component in the same graph, but where the edges are undirected. So for simplicity we consider 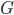 as an undirected graph.
as an undirected graph.
Algorithm description
On the graph we run a pre-order Depth First Search (DFS) visit where for any node 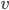 we assign 2 values, let's call it
we assign 2 values, let's call it pre and low. pre represent the instant when the node is visited and low the instant of the lowest reachable node from 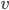 .
.
The visit works in this way:
At every step of the visit both pre and low of 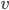 are set to the next value of
are set to the next value of pre. Then if we find that a cycle is being closed we set low to pre of the start cycle node. low value is transmitted to parent through DFS backtracking.
When the DFS finish for every couple of nodes 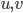 such that
such that 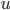 and
and 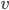 are neighbor and
are neighbor and low value of 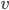 is greater or equal to the
is greater or equal to the pre value of 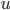 then
then 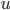 is an articulation point.
is an articulation point.
For this there is an exception: the root of the DFS spanning tree is an articulation point only if it has more than 1 children
Example
(In the graph P obviously means pre and L means low)
At first pre and low of every vertex are set to a default value (let's say -1)
We start from node 0 and set his pre and low
We go to node 1 and set his pre and low
We can go to 2 or 3, we decide to go to 2 and set his pre and low
We can go to 4 or 5, we decide to go to 4 and set his pre and low

We go to 3 and set his pre and low
We see that 1 is alredy visited; that means it is a cycle, so we update low of 3 to pre of 1

Through backtrack we return to 4 and update his low value

Through backtrack we return to 2 and update his low value
Now we go to 5 and set his pre and low
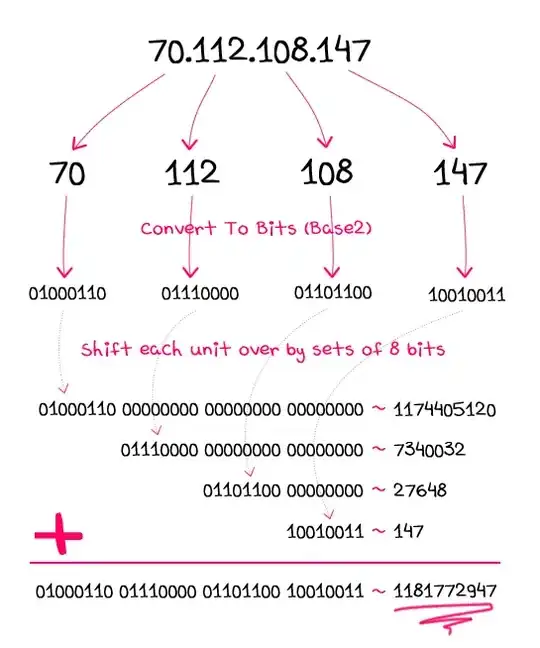
Through backtrack we return to 2, but there's nothing to do.
We returned from 5 so his low value is fixed and is greater than pre value of 2; so 2 is an articulation point
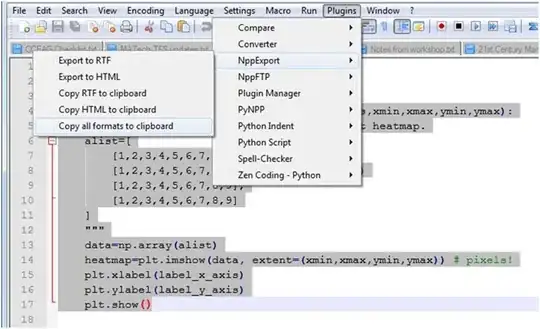
Through backtrack we return to 1, and there's nothing to do.
We returned from 2 so his low value is fixed and is equal to the pre value of 1; so 1 is an articulation point
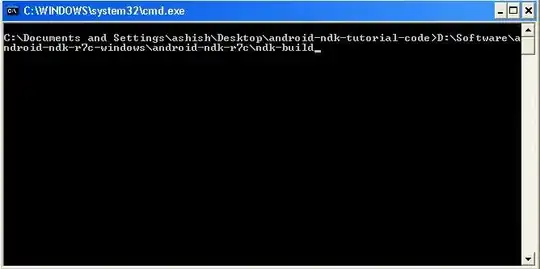
Through backtrack we return to 0, but there's nothing to do.
We returned from 1 so his low value is fixed and is greater than pre value of 0; but 0 is the root and has only one child; so it isn't an articulation point

So we have found the answer: [1, 2]
Code
Here is a simple really easy to understand snippet of code (C++) extracted from Competitive Programming Handbook by S. Halim and F. Halim and modified by me.
It is not very adapt to "real word application" (for example because it uses global variables) but it is ok for competitive programming and explaining due to his brevity and clearness.
const int UNVISITED = -1;
vector<int> dfs_low;
vector<int> dfs_pre;
int dfsNumberCounter;
int rootChildren;
vector<vector<int>> AdjList;
vector<int> articulation_vertex;
// This function is the DFS that implement Tarjan algoritm
void articulationPoint(int u) {
dfs_low[u] = dfs_pre[u] = dfsNumberCounter++; // dfs_low[u] <= dfs_pre[u]
for (int j = 0; j < (int)AdjList[u].size(); j++) {
int v = AdjList[u][j];
if (dfs_pre[v] == UNVISITED) { // a tree edge
dfs_parent[v] = u;
if (u == dfsRoot) rootChildren++; // special case if u is a root
articulationPoint(v);
if (dfs_low[v] >= dfs_pre[u]) // for articulation point
articulation_vertex[u] = true; // store this information first
dfs_low[u] = min(dfs_low[u], dfs_low[v]); // update dfs_low[u]
}
else if (v != dfs_parent[u]) // a back edge and not direct cycle
dfs_low[u] = min(dfs_low[u], dfs_pre[v]); // update dfs_low[u]
} }
// Some driver code
int main() {
... //Init of variables and store of the graph inside AdjList is omitted
... // V is the number of nodes
dfsNumberCounter = 0;
dfs_pre.assign(V, UNVISITED);
dfs_low.assign(V, 0);
dfs_parent.assign(V, 0);
articulation_vertex.assign(V, 0);
rootChildren = 0;
articulationPoint(0);
if (root_children > 1) {
articulation_vertex[0] = false;
}
printf("Articulation Points:\n");
for (int i = 0; i < V; i++)
if (articulation_vertex[i])
printf(" Vertex %d\n", i);
}

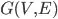 we want to find all the
we want to find all the 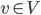 such that if
such that if 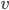 is removed from
is removed from 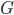 the graph become disconnected
the graph become disconnected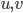 such that
such that 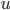 and
and 











