Brzozowski's algorithm
Brzozowski's algorithm is clearer written as:
minimized_DFA = subset(reverse(subset(reverse(NFA))))
where subset denotes subset construction (also known as powerset construction). Subset construction builds a DFA by simulating all transitions for each equivalent set of states (due to epsilon transitions) in the NFA.
Reversing an NFA involves these steps:
- Reverse the direction of all transition edges in the NFA.
- Create a new starting state that has epsilon transitions to all accepting states in the NFA.
- Mark all accepting states as non-accepting in the NFA.
- Make the old starting state the new accepting state.
Steps 2-4 effectively swaps the roles of accepting and starting states.
Brzozowski's algorithm example
Here's an example of minimizing a DFA based on a Udacity quiz for a compilers course (the steps are the same with an NFA as initial input).
Initial DFA:
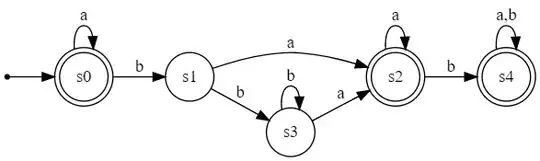
This DFA accepts strings like {"", "a", "aa", "aaa", "aaabba", "ba", "bab", "ababa", "ababb"} and rejects strings like {"b", "ab", "aab", "aabb", "bb", "bbb"}. In other words, it rejects strings that have a "b" unless they also have a "ba" substring. It's pretty obvious that s1-s3 and s2-s4 are redundant.
Step 1: reverse(DFA):
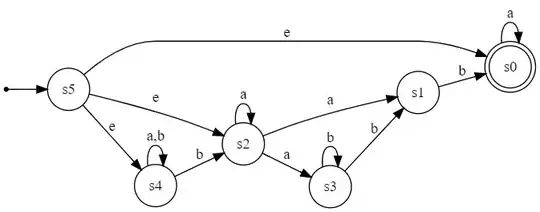
Step 2: subset(reverse(DFA)):
Run subset construction to build a table of DFA states to represent possible transitions from each unique epsilon closure (^ denotes a start state, $ denotes an accepting state):
A = e-closure({s5}) = {s0,s2,s4}
B = e-closure({s0,s1,s2,s3,s4}) = {s0,s1,s2,s3,s4}
C = e-closure({s2,s4}) = {s2,s4}
D = e-closure({s1,s2,s3,s4}) = {s1,s2,s3,s4}
a b
-----------
A^$ B C
B$ B B
C D C
D D B

Step 3: reverse(subset(reverse(DFA))):
Reverse the DFA. After eliminating common prefixes, another pass enables elimination of common suffixes.
Step 4: subset(reverse(subset(reverse(DFA)))):
Run subset construction one more time to minimize the NFA.
A = e-closure({E}) = {A,B}
B = e-closure({B,D}) = {B,D}
C = e-closure({A,B,C,D} = {A,B,C,D}
a b
--------
A^$ A B
B C B
C$ C C
References:
Graphviz code for above diagrams:
// initial DFA
digraph G {
rankdir=LR;
size="8,5"
node [shape=point]; qi;
node [shape=doublecircle]; s0 s2 s4;
node [shape=circle];
qi -> s0;
s0 -> s0 [label="a"];
s0 -> s1 [label="b"];
s1 -> s2 [label="a"];
s2 -> s2 [label="a"];
s2 -> s4 [label="b"];
s4 -> s4 [label="a,b"];
s1 -> s3 [label="b"];
s3 -> s3 [label="b"];
s3 -> s2 [label="a"];
}
// reverse(DFA)
digraph G {
rankdir=LR;
size="8,5"
node [shape=point]; qi;
node [shape=doublecircle]; s0;
node [shape=circle];
qi -> s5;
s0 -> s0 [label="a"];
s1 -> s0 [label="b"];
s2 -> s1 [label="a"];
s2 -> s2 [label="a"];
s4 -> s2 [label="b"];
s4 -> s4 [label="a,b"];
s3 -> s1 [label="b"];
s3 -> s3 [label="b"];
s2 -> s3 [label="a"];
s5 -> s2 [label="e"];
s5 -> s0 [label="e"];
s5 -> s4 [label="e"];
}
// subset(reverse(DFA))
digraph G {
rankdir=LR;
size="8,5"
node [shape=point]; qi;
node [shape=doublecircle]; A B;
node [shape=circle];
qi -> A;
A -> B [label="a"];
A -> C [label="b"];
B -> B [label="a,b"];
D -> B [label="b"];
C -> D [label="a"];
C -> C [label="b"];
D -> D [label="a"];
}
// reverse(subset(reverse(DFA)))
digraph G {
rankdir=LR;
size="8,5"
node [shape=point]; qi;
node [shape=doublecircle]; A;
node [shape=circle];
qi -> E;
B -> A [label="a"];
C -> A [label="b"];
B -> B [label="a,b"];
B -> D [label="b"];
D -> C [label="a"];
C -> C [label="b"];
D -> D [label="a"];
E -> A [label="e"];
E -> B [label="e"];
}
// subset(reverse(subset(reverse(DFA))))
digraph G {
rankdir=LR;
size="8,5"
node [shape=point]; qi;
node [shape=doublecircle]; A C;
node [shape=circle];
qi -> A;
A -> A [label="a"];
A -> B [label="b"];
B -> B [label="b"];
B -> C [label="a"];
C -> C [label="a,b"];
}




