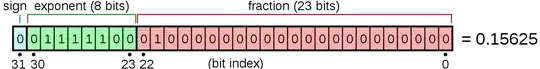Problem of a simple float number serialization example

Question

I am reading the Serialization section of a tutorial http://beej.us/guide/bgnet/html/#serialization .

And I am reviewing the code which Encode the number into a portable binary form.

#include <stdint.h>

uint32_t htonf(float f)
{
    uint32_t p;
    uint32_t sign;

    if (f < 0) { sign = 1; f = -f; }
    else { sign = 0; }

    p = ((((uint32_t)f)&0x7fff)<<16) | (sign<<31); // whole part and sign
    p |= (uint32_t)(((f - (int)f) * 65536.0f))&0xffff; // fraction

    return p;
}

float ntohf(uint32_t p)
{
    float f = ((p>>16)&0x7fff); // whole part
    f += (p&0xffff) / 65536.0f; // fraction

    if (((p>>31)&0x1) == 0x1) { f = -f; } // sign bit set

    return f;
}

I ran into problems with this line p = ((((uint32_t)f)&0x7fff)<<16) | (sign<<31); // whole part and sign .

According to the original code comments, this line extracts the whole part and sign, and the next line deals with fraction part.

Then I found an image about how float is represented in memory and started the calculation by hand.

From Wikipedia Single-precision floating-point format:

So I then presumed that whole part == exponent part.

But this (uint32_t)f)&0x7fff)<<16) is getting the last 15bits of the fraction part, if based on the image above.

Now I get confused, where did I get wrong?

Answer 1

It's important to realize what this code is not. This code does not do anything with the individual bits of a float value. (If it did, it wouldn't be portable and machine-independent, as it claims to be.) And the "portable" string representation it creates is fixed point, not floating point.

For example, if we use this code to convert the number -123.125, we will get the binary result

10000000011110110010000000000000

or in hexadecimal

807b2000

Now, where did that number 10000000011110110010000000000000 come from? Let's break it up into its sign, whole number, and fractional parts:

1 000000001111011 0010000000000000

The sign bit is 1 because our original number was negative. 000000001111011 is the 15-bit binary representation of 123. And 0010000000000000 is 8192. Where did 8192 come from? Well, 8192 ÷ 65536 is 0.125, which was our fractional part. (More on this below.)

How did the code do this? Let's walk through it step by step.

(1) Extract sign. That's easy: it's the ordinary test if(f < 0).

(2) Extract whole-number part. That's also easy: We take our floating-point number f, and cast it to type unint32_t. When you convert a floating-point number to an integer in C, the behavior is pretty obvious: it throws away the fractional part and gives you the integer. So if f is 123.125, (uint32_t)f is 123.

(3) Extract fraction. Since we've already got the integer part, we can isolate the fraction by starting with the original floating-point number f, and subtracting the integer part. That is, 123.125 - 123 = 0.125. Then we multiply the fractional part by 65536, which is 2¹⁶.

It may not be obvious why we multiplied by 65536 and not some other number. In one sense, it doesn't matter what number you use. The goal here is to take a fractional number f and turn it into two integers a and b such that we can recover the fractional number f again later (although perhaps approximately). The way we're going to recover the fractional number f again later is by computing

a + b / x

where x is, well, some other number. If we chose 1000 for x, we'd break 123.125 up into a and b values of 123 and 125. We're choosing 65536, or 2¹⁶, for x because that lets us make maximal use of the 16 bits we've allocated for the fractional part in our representation. Since x is 65536, b has to be some number we can divide by 65536 in order to get 0.125. So since b / 65536 = 0.125, by simple algebra we have b = 0.125 * 65536. Make sense?

Anyway, let's now look at the actual code for performing steps 1, 2, and 3.

if (f < 0) { sign = 1; f = -f; }

Easy peasy. If f is negative, our sign bit will be 1, and we want the rest of the code to operate on the positive version of f.

p = ((((uint32_t)f)&0x7fff)<<16) | (sign<<31);

As mentioned, the important part here is (uint32_t)f, which just grabs the integer (whole-number) part of f. The bitmask & 0x7fff extracts the low-order 15 bits of it, throwing anything else away. (This is since our "portable representation" only allocates 15 bits for the whole-number part, meaning that numbers greater than 2¹⁵-1 or 32767 can't be represented). The shift << 16 moves it into the high half of the eventual unint32_t result, where it belongs. And then | (sign<<31) takes the sign bit and puts it in the high-order position where it belongs.

p |= (uint32_t)(((f - (int)f) * 65536.0f))&0xffff; // fraction

Here, (int)f recomputes the integer (whole-number) part of f, and then f - (int)f extracts the fraction. We multiply it by 65536, as explained above. There may still be a fractional part (even after the multiplication, that is), so we cast to (uint32_t) again to throw that away, retaining only the integer part. We can only handle 16 bits of fraction, so we extract those bits (discarding anything else) with & 0xffff, although this should be unnecessary since we started with a positive fractional number less than 1, and multiplied it by 65536, so we should end up with a positive number less than 65536, i.e. we shouldn't have a number that won't exactly fit in 16 bits. Finally, the p |= operation stuffs these 16 bits we've just computed into the low-order half of p, and we're done.

---

Addendum: It may still not be obvious where the number 65536 came from, and why that was used instead of 10000 or some other number. So let's review two key points: we're ultimately dealing with integers here. Also, in one sense, the number 65536 actually was pretty arbitrary.

At the end of the day, any bit pattern we're working with is "really" just an integer. It's not a character, or a floating-point number, or a pointer — it's just an integer. If it has N bits, it represents integers from 0 to 2^N-1.

In the fixed-point representation we're using here, there are three subfields: a 1-bit sign, a 15-bit whole-number part, and a 16-bit fraction part.

The interpretation of the sign and whole-number parts is obvious. But the question is: how shall we represent a fraction using a 16-bit integer?

And the answer is, we pick a number, almost any number, to divide by. We can call this number a "scaling factor".

We really can pick almost any number. Suppose I chose the number 3467 as my scaling factor. Here is now I would then represent several different fractions as integers:

    ½ → 1734/3467 → 1734
    ⅓ → 1155/3467 → 1155
    0.125 → 433/3467 → 433

So my fractions ½, ⅓, and 0.125 are represented by the integers 1734, 1155, and 433. To recover my original fractions, I just divide by 3467:

    1734 → 1734 ÷ 3467 → 0.500144
    1155 → 1155 ÷ 3467 → 0.333141
    433 → 1734 ÷ 3467 → 0.124891

Obviously I wasn't able to recover my original fractions exactly, but I came pretty close.

The other thing to wonder about is, where does that number 3467 "live"? If you're just looking at the numbers 1734, 1155, and 433, how do you know you're supposed to divide them by 3467? And the answer is, you don't know, at least, not just by looking at them. 3567 would have to be part of the definition of my silly fractional number format; people would just have to know, because I said so, that they had to multiply by 3467 when constructing integers to represent fractions, and divide by 3467 when recovering the original fractions.

And the other thing to look at is what the implications are of choosing various different scaling factors. The first thing is that, since in the end we're going to be using a 16-bit integer for the fractional representation, we absolutely can't use a scaling factor any greater than 65536. If we did, sometimes we'd end up with an integer greater than 65535, and it wouldn't fit in 16 bits. For example, suppose we tried to use a scaling factor of 70000, and suppose we tried to represent the fraction 0.95. Now, 0.95 is equal to 66500/70000, so our integer would be 66500, but that doesn't fit in 16 bits.

On the other hand, it turns out that ideally we don't want to use a number less than 65536, either. The smaller a number we use, the more of our 16-bit fractional representation we'll waste. When I chose 3467 in my silly example a little earlier, that meant I would represent fractions from 0/3467 = 0.00000 and 1/3467 = 0.000288 up to 3466/3467 = 0.999711. But I'd never use any of the integers from 3467 through 65536. They'd be wasted, and by not using them, I'd unnecessarily limit the precision of the fractions I could represent.

The "best" (least wasteful) scaling factor to use is 65536, although there's one other consideration, namely, which fractions do you want to be able to represent exactly? When I used 3467 as my scaling factor, I couldn't represent any of my test numbers ½, ⅓, or 0.125 exactly. If we use 65536 as the scaling factor, it turns out that we can represent fractions involving small powers of two exactly — that is, halves, quarters, eights, sixteenths, etc. — but not any other fractions, and in particular not most of the decimal fractions like 0.1. If we wanted to be able to represent decimal fractions exactly, we would have to use a scaling factor that was a power of 10. The largest power of 10 that will fit in 16 bits is 10000, and that would indeed let us exactly represent decimal fractions as small as 0.00001, although we'd waste about 5/6 (or 85%) of our 16-bit fractional range.

So if we wanted to represent decimal fractions exactly, without wasting precision, the inescapable conclusion is that we should not have allocated 16 bits for our fraction field in the first place. Better choices would have been 10 bits (ideal scaling factor 1024, we'd use 1000, wasting only 2%) or 20 bits (ideal scaling factor 1048576, we'd use 1000000, wasting about 5%).

Answer 2

The relevant excerpts from the page are

The thing to do is to pack the data into a known format and send that over the wire for decoding. For example, to pack floats, here’s something quick and dirty with plenty of room for improvement

and

On the plus side, it’s small, simple, and fast. On the minus side, it’s not an efficient use of space and the range is severely restricted—try storing a number greater-than 32767 in there and it won’t be very happy! You can also see in the above example that the last couple decimal places are not correctly preserved.

The code is presented only as an example. It is really quick and dirty, because it packs and unpacks the float as a fixed point number with 16 bits for fractions, 15 bits for integer magnitude and one for sign. It is an example and does not attempt to map floats 1:1.

It is in fact rather incredibly stupid algorithm: It can map 1:1 all IEEE 754 float32s within magnitude range ~256...32767 without losing a bit of information, truncate the fractions in floats in range 0...255 to 16 bits, and fail spectacularly for any number >= 32768. And NaNs.

---

As for the endianness problem: for any protocol that does not work with integers >= 32 bits intrinsically, someone needs to decide how to again serialize these integers into the other format. For example in the Internet at lowest levels data consists of 8-bit octets.

There are 24 obvious ways mapping a 32-bit unsigned integer into 4 octets, of which 2 are now generally used, and some more historically. Of course there are a countably infinite (and exponentially sillier) ways of encoding them...