Very small populations/state variables to zero in differential equation solutions

Question

I'm posting because I am numerically solving ordinary differential equations and would like to constrain the state variables. In sum, I'm a biologist modeling populations and would like for the populations to go extinct when they become really small.

When I run my models populations can become very, very small (e.g., 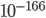$10^{-166}$ ), but never go to 0. It's important for me that they do so, so I can calculate extinction. But more realistically, when a population is at a density that is considerably smaller than there are at atoms on Earth, that's not too realistic ;)

Even in the simple 2-species enemy-victim model like the following reaches densities of 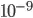$10^{-9}$ that I would like to be interpreted as 0.

library(package = "deSolve")

lv <- function(times, state, parms) {
    with(as.list(c(state, parms)), {
    dR <- 2*R - 0.5*R*C
    dC <- 0.2*R*C - 0.6*C
    return(list(c(dR, dC)))
    })
}

time_vec <- seq(from = 0, to = 100, length.out = 1e4)
y_0 <- c(R = 50, C = 20)

out <- ode(y = y_0, times = time_vec, func = lv, parms = NULL, method = "lsoda")
min(out[,-1])
plot(x = out[,2], y = out[,3], type = "l")

I'd ideally like to see how extinction can be modeled using the solver `deSolve' in R, but any help directing me towards general answers/names for this type of problem would also be very appreciated.

P.S. This is similar to a post on wanting to replace negative values with 0 (link), but different because I want the populations not to just be non-negative, but stay at 0 infinitely. But also, there wasn't a good answer on how to do that in this post.

Can you just add an `if` statement to your function that sets the value to 0 if the calculated value is less than your preferred cutoff? e.g. `if(dR < 1e-5) {dR <- 0}` — benc, Dec 03 '19 at 19:50
Thanks @benc The problem with that is that dR calculates the derivative, so although that is equal to 0, the population (state variable) remains positive and not at 0. This results in undesirable effects, like not going extinct. — Chris Moore, Dec 03 '19 at 20:10
A differential equation system works with continuous time and continuous state variables, so it is unlikely to approach exactly zero. You may consider to use discrete models instead: difference equations or individual-based models. — tpetzoldt, Dec 03 '19 at 20:50
... another (pragmatic) option would be an event with root finding. If a state drops down below a critical value, an event is triggered that sets the state to zero. However, this is really really a very pragmatic approach. — tpetzoldt, Dec 03 '19 at 20:52
Thanks @tpetzoldt The mathematical equations we are analyzing are in continuous time, so it's important to keep them in that format. The events sound promising. My understanding was that events were triggered at specific times rather than values of the state variables. How could that be incorporated into an example like the one above? — Chris Moore, Dec 03 '19 at 21:05
I'm pretty sure you can use `deSolve::lsodar` to trigger an event based on the state of the system. — Ben Bolker, Dec 03 '19 at 21:17
It is doubtful that you will see extinction in this Lotka-Voltera model, since it has periodic solutions that thus have a positive minimum distance from the coordinate axes. Of course, if you add more terms to be more realistic, this pattern is destroyed and you can get anything from stable limit cycles to extinction. — Lutz Lehmann, Dec 04 '19 at 19:37
Thanks @dr-lutz-lehmann Agreed. This is just a simple example that I thought people would understand, and I'm not actually analyzing it. It nevertheless resulted in my question being answered. Although the analytical model never results in extinction, the actual biological system would go extinct if densities became sufficiently small. That's a discrepancy between a model and reality that I am trying to mend. — Chris Moore, Dec 04 '19 at 20:01
I agree with @dr-lutz-lehmann It is wise to follow a general theory or model. So I need to point out that we leave this when using events. Another way would indeed be to add more terms, and just another (my preferred one) to change the context: to employ individual-based models for example. — tpetzoldt, Dec 04 '19 at 22:36
@tpetzoldt I agree too. I have a 2-variable model that I can analyze, which follows the continuous-time theory. But, I want to embed the 2 variables in a much larger system with different dynamics and simulate what happens since there is no analytical solution. The two uses are qualitatively different, but I wish to remain consistent conceptually, and care more about qualitative dynamics than accuracy. Thanks for the comments, and I hope this is a bit more clear. — Chris Moore, Dec 05 '19 at 21:39

score 2 · Accepted Answer · answered Dec 03 '19 at 21:42

Here an example. As said, very pragmatic.

library(package = "deSolve")

lv <- function(times, state, parms) {
  with(as.list(c(state, parms)), {
    dR <- 2*R - 0.5*R*C
    dC <- 0.2*R*C - 0.6*C
    return(list(c(dR, dC)))
  })
}

time_vec <- seq(from = 0, to = 100, length.out = 1e4)
y_0 <- c(R = 50, C = 20)
out <- ode(y = y_0, times = time_vec, func = lv, parms = NULL, method = "lsoda")
min(out[,-1])

eps <- 1e-2
## event triggered if state variable <= eps
rootfun <- function (t, y, pars) {
  return(y - eps)
}

## sets state variable = 0
eventfun <- function(t, y, pars) {
  if (y[1] <= eps) y[1] <- 0
  if (y[2] <= eps) y[2] <- 0
  return(y)
}

out1 <- ode(y = y_0, times = time_vec, func = lv, parms = NULL, method = "lsoda",
           rootfun = rootfun,
           events = list(func = eventfun, root = TRUE))

plot(out, out1)
min(out1[,-1])

Very small populations/state variables to zero in differential equation solutions

1 Answers1