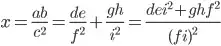Hundreds of times faster than yours and without your floating point issues.
Thousands of times faster than kaya3's O(n²) solution.
I ran it until MAX_NUM = 4,000,000 and found no results. Took about 12 minutes.
Exploit the special numbers.
This is not just an ordinary 3SUM. The numbers are special and we can exploit it. They have the form ab/c², where (a,b,c) is a primitive Pythagorean triple.
So let's say we have a number x=ab/c² and we want to find two other such numbers that add up to x:
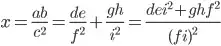
After canceling, the denominators c² and (fi)² become c²/k and (fi)²/m (for some integers k and m) and we have c²/k = (fi)²/m. Let p be the largest prime factor of c²/k. Then p also divides (fi)²/m and thus f or i. So at least one of the numbers de/f² and gh/i² has a denominator divisible by p. Let's call that one y, and the other one z.
So for a certain x, how do we find fitting y and z? We don't have to try all numbers for y and z. For y we only try those whose denominator is divisible by p. And for z? We compute it as x-y and check whether we have that number (in a hashset).
How much does it help? I had my solution count how many y-candidates there are if you naively try all (smaller than x) numbers and how many y-candidates there are with my way and how much less that is:
MAX_NUM naive mine % less
--------------------------------------------------
10,000 1,268,028 17,686 98.61
100,000 126,699,321 725,147 99.43
500,000 3,166,607,571 9,926,863 99.69
1,000,000 12,662,531,091 30,842,188 99.76
2,000,000 50,663,652,040 96,536,552 99.81
4,000,000 202,640,284,036 303,159,038 99.85
Pseudocode
The above description in code form:
h = hashset(numbers)
for x in the numbers:
p = the largest prime factor in the denominator of x
for y in the numbers whose denominator is divisible by p:
z = x - y
if z is in h:
output (x, y, z)
Benchmarks
Times in seconds for various MAX_NUM and their resulting n:
MAX_NUM: 10,000 100,000 500,000 1,000,000 2,000,000 4,000,000
=> n: 1,593 15,919 79,582 159,139 318,320 636,617
--------------------------------------------------------------------------------
Original solution 1.6 222.3 - - - -
My solution 0.05 1.6 22.1 71.0 228.0 735.5
kaya3's solution 29.1 2927.1 - - - -
Complexity
This is O(n²), and maybe actually better. I don't understand the nature of the numbers well enough to reason about them, but the above benchmarks do make it look substantially better than O(n²). For quadratic runtime, going from n=318,320 to n=636,617 you'd expect a runtime increase of factor (636,617/318,320)² ≈ 4.00, but the actual increase is only 735.5/228.0 ≈ 3.23.
I didn't run yours for all sizes, but since you grow at least quadratically, at MAX_NUM=4,000,000 your solution would take at least 222.3 * (636,617/15,919)² = 355,520 seconds, which is 483 times slower than mine. Likewise, kaya3's would be about 6365 times slower than mine.
Lose time with this one weird trick
Python's Fraction class is neat, but it's also slow. Especially its hashing. Converting to tuple and hashing that tuple is about 34 times faster:
>set SETUP="import fractions; f = fractions.Fraction(31459, 271828)"
>python -m timeit -s %SETUP% -n 100000 "hash(f)"
100000 loops, best of 5: 19.8 usec per loop
>python -m timeit -s %SETUP% -n 100000 "hash((f.numerator, f.denominator))"
100000 loops, best of 5: 581 nsec per loop
Its code says:
[...] this method is expensive [...] In order to make sure that the hash of a Fraction agrees with the hash of a numerically equal integer, float or Decimal instance, we follow the rules for numeric hashes outlined in the documentation.
Other operations are also somewhat slow, so I don't use Fraction other than for output. I use (numerator, denominator) tuples instead.
The solution code
from math import gcd
def solve_stefan(triples):
# Prime factorization stuff
largest_prime_factor = [0] * (MAX_NUM + 1)
for i in range(2, MAX_NUM+1):
if not largest_prime_factor[i]:
for m in range(i, MAX_NUM+1, i):
largest_prime_factor[m] = i
def prime_factors(k):
while k > 1:
p = largest_prime_factor[k]
yield p
while k % p == 0:
k //= p
# Lightweight fractions, represented as tuple (numerator, denominator)
def frac(num, den):
g = gcd(num, den)
return num // g, den // g
def sub(frac1, frac2):
a, b = frac1
c, d = frac2
return frac(a*d - b*c, b*d)
class Key:
def __init__(self, triple):
a, b, c = map(int, triple)
self.frac = frac(a*b, c*c)
def __lt__(self, other):
a, b = self.frac
c, d = other.frac
return a*d < b*c
# The search. See notes under the code.
seen = set()
supers = [[] for _ in range(MAX_NUM + 1)]
for triple in sorted(triples, key=Key):
a, b, c = map(int, triple)
x = frac(a*b, c*c)
denominator_primes = [p for p in prime_factors(c) if x[1] % p == 0]
for y in supers[denominator_primes[0]]:
z = sub(x, y)
if z in seen:
yield tuple(sorted(Fraction(*frac) for frac in (x, y, z)))
seen.add(x)
for p in denominator_primes:
supers[p].append(x)
Notes:
- I go through the triples in increasing fraction value, i.e., increasing x value.
- My
denominator_primes is the list of prime factors of x's denominator. Remember that's c²/k, so its prime factors must also be prime factors of c. But k might've cancelled some, so I go through the prime factors of c and check whether they divide the denominator. Why so "complicated" instead of just looking up prime factors of c²/k? Because that can be prohibitively large.
denominator_primes is descending, so that p is simply denominator_primes[0]. Btw, why use the largest? Because larger means rarer means fewer y-candidates means faster.supers[p] lists the numbers whose denominator is divisible by p. It's used to get the y-candidates.- When I'm done with x, I use
denominator_primes to put x into the supers lists, so it can then be the y for future x values.
- I build the
seen and supers during the loop (instead of before) to keep them small. After all, for x=y+z with positive numbers, y and z must be smaller than x, so looking for larger ones would be wasteful.
Verification
How do you verify your results if there aren't any? As far as I know, none of our solutions have found any. So there's nothing to compare, other than the nothingness, which is not exactly convincing. Well, my solution doesn't depend on the Pythagoreanness, so I created a set of just primitive triples and checked my solution's results for that. It computed the same 25,336 results as a reference implementation:
def solve_reference(triples):
fractions = {Fraction(int(a) * int(b), int(c)**2)
for a, b, c in triples}
for x, y in combinations_with_replacement(sorted(fractions), 2):
z = x + y
if z in fractions:
yield x, y, z
MIN_NUM = 2
MAX_NUM = 25
def triples():
return list((a, b, c)
for a, b, c in combinations(range(MIN_NUM, MAX_NUM+1), 3)
if gcd(a, gcd(b, c)) == 1)
print(len(triples()), 'input triples')
expect = set(solve_reference(triples()))
print(len(expect), 'results')
output = set(solve_stefan(triples()))
print('output is', ('wrong', 'correct')[output == expect])
Output:
1741 input triples
25336 results
output is correct