Fill between subplots with matplotlib cmap

Question

I have 2 line plots on the same figure, plotted from pandas dataframes.

I want to fill between them with a gradient/colour map of sorts.

I understand I can do this with a cmap, only it will not work for me (see code below).

General example I found are filling between x axis and line, i do not want that and also i am interested in simplest solution possible for this as i am a begginer at this and complicated, though maybe better code will just make it more confusing honestly.

Code for which fill is plain blue:

import matplotlib.pyplot as plt
import pandas as pd

ax = plt.gca()

df0.plot(kind='line', x='something', y='other', color='orange', ax=ax, legend=False, figsize=(20,10))
df1.plot(kind='line', x='something', y='other2', color='c', ax=ax, legend=False, figsize=(20,10))

ax.fill_between(x=df0['daysInAYear'], y1=df0['other'], y2 = df1['other2'], alpha=0.2, cmap=plt.cm.get_cmap("winter"))
plt.show()

EDIT/UPDATE: DATA EXAMPLE other is ALWAYS >= other2

other  other2  something (same for both)
15.6    -16.0      1
13.9    -26.7      2
13.3    -26.7      3
10.6    -26.1      4
12.8    -15.0      5

Final graph example:

I would like the fill to go from orange on top to blue at the bottom

@ryuuzako Have you had a chance to try the method in my answer? — William Miller, Jan 09 '20 at 22:33
@WilliamMiller hey, i didn't get around it but i promise once i do that i will update here! — ryuuzako, Jan 13 '20 at 18:48

William Miller · Answer 1 · 2020-04-26T20:24:26.633

Edit

In response to the edited question, here is an alternative approach which does the gradient vertically but doesn't use imshow.

import matplotlib.pyplot as plt
from  matplotlib import colors, patches
import numpy as np
import pandas as pd

n = 100
nc = 100

x = np.linspace(0, np.pi*5, n)
y1 = [-50.0]
y2 = [50.0]
for ii in range(1, n):
    y1.append(y1[ii-1] + (np.random.random()-0.3)*3)
    y2.append(y2[ii-1] + (np.random.random()-0.5)*3)
y1 = np.array(y1)
y2 = np.array(y2)
z = np.linspace(0, 10, nc)
normalize = colors.Normalize(vmin=z.min(), vmax=z.max())
cmap = plt.cm.get_cmap('winter')

fig, ax = plt.subplots(1)
for ii in range(len(df['x'].values)-1):
    y = np.linspace(y1[ii], y2[ii], nc)
    yn = np.linspace(y1[ii+1], y2[ii+1], nc)
    for kk in range(nc - 1):
        p = patches.Polygon([[x[ii], y[kk]], 
                             [x[ii+1], yn[kk]], 
                             [x[ii+1], yn[kk+1]], 
                             [x[ii], y[kk+1]]], color=cmap(normalize(z[kk])))
        ax.add_patch(p)

plt.plot(x, y1, 'k-', lw=1)
plt.plot(x, y2, 'k-', lw=1)
plt.show()

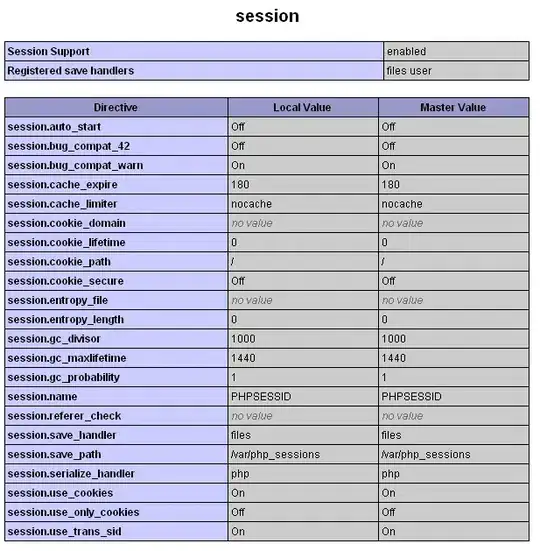
The idea here being similar to that in my original answer, except the trapezoids are divided into nc pieces and each piece is colored separately. This has the advantage of scaling correctly for varying y1[ii], y2[ii] distances, as shown in this comparison,

It does, however, have the disadvantages of being much, much slower than imshow or the horizontal gradient method and of being unable to handle 'crossing' correctly.

The code to generate the second image in the above comparison:

import matplotlib.pyplot as plt
import numpy as np
from matplotlib import patches
from matplotlib.path import Path

x = np.linspace(0, 10, n)
y1 = [-50.0]
y2 = [50.0]
for ii in range(1, n):
    y1.append(y1[ii-1] + (np.random.random()-0.2)*3)
    y2.append(y2[ii-1] + (np.random.random()-0.5)*3)
y1 = np.array(y1)
y2 = np.array(y2)

verts = np.vstack([np.stack([x, y1], 1), np.stack([np.flip(x), np.flip(y2)], 1)])
path = Path(verts)

patch = patches.PathPatch(path, facecolor='k', lw=2, alpha=0.0)
plt.gca().add_patch(patch)

plt.imshow(np.arange(10).reshape(10,-1), cmap=plt.cm.winter, interpolation="bicubic",
             origin='upper', extent=[0,10,-60,60], aspect='auto', clip_path=patch, 
             clip_on=True)
plt.show()

Original

This is a bit of a hack, partly based on the answers in this question. It does seem to work fairly well but works best with higher density along the x axis. The idea is to call fill_between separately for each trapezoid corresponding to x pairs, [x[ii], x[ii+1]]. Here is a complete example using some generated data

import matplotlib.pyplot as plt
from  matplotlib import colors
import numpy as np
import pandas as pd

n = 1000

X = np.linspace(0, np.pi*5, n)
Y1 = np.sin(X)
Y2 = np.cos(X)
Z = np.linspace(0, 10, n)
normalize = colors.Normalize(vmin=Z.min(), vmax=Z.max())
cmap = plt.cm.get_cmap('winter')

df = pd.DataFrame({'x': X, 'y1': Y1, 'y2': Y2, 'z': Z})
x = df['x'].values
y1 = df['y1'].values
y2 = df['y2'].values
z = df['z'].values

for ii in range(len(df['x'].values)-1):
    plt.fill_between([x[ii], x[ii+1]], [y1[ii], y1[ii+1]], 
                     [y2[ii], y2[ii+1]], color=cmap(normalize(z[ii])))

plt.plot(x, y1, 'k-', x, y2, 'k-')
plt.show()

This can be generalized to a 2 dimensional color grid but would require non-trivial modification

Since imshow is much faster than plotting hundreds of patches it's not really clear why one should try to avoid using it. — ImportanceOfBeingErnest, Jan 04 '20 at 22:17
@ImportanceOfBeingErnest Perhaps I was unclear. I’m not saying `imshow` ought to be avoided, I’m simply saying this is a way to do it which does not use `imshow`. — William Miller, Jan 04 '20 at 23:48
@ImportanceOfBeingErnest The reason to use this method over `imshow`, as I see it, is outlined by [this](https://i.stack.imgur.com/WWpn3.png) and [this](https://i.stack.imgur.com/4aJMF.png) where clipping the `imshow` does not produce the correct gradient with variable `y1` and `y2` distances or when `y1` and/or `y2` have with `x`. How would you use `imshow` to produce the correct gradient in these cases? — William Miller, Jan 16 '20 at 05:30
The question remains a bit unclear on how exactly the gradient is supposed to look (i.e. if it is a gradient *per x data point*, or a global gradient. The latter would make much more sense though(?)). In any case, you can always create an image that looks like the desired outcome, so not sure what exactly is the problem. — ImportanceOfBeingErnest, Jan 16 '20 at 12:04
Could you please provide the code based on imshow, for horizontal gradient method where the colours defined with y value only? I have exactly the same question, but I find the answer unsatisfactory. Is this the only way to do the colour gradient inside fill_between? — Vladimir, Apr 25 '20 at 17:55
I meant for the _vertical_ gradient, like in the right panel of the above comparison. — Vladimir, Apr 26 '20 at 01:04
@Vladimir I have added the code for the `plt.imshow` approach — William Miller, Apr 26 '20 at 20:25
Thanks! That is also much more elegant and faster approach. I understand the first image has different prior, but I can not imagine any reasonable use for such varying vertical gradient in practice, except that it is prettier. — Vladimir, May 09 '20 at 00:45

Fill between subplots with matplotlib cmap

1 Answers1

Edit

Original