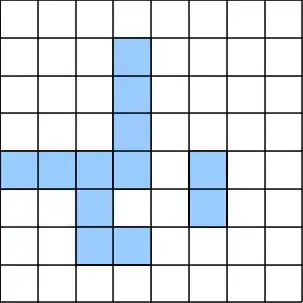
I have NxM board. I want to add K obstacles to it, but in a way so it is still possible to get from each empty space to every other empty space. I want it to look something like this
where blue squares are obstacles.
In other words, I have a graph grid and I want to randomly remove K vertices from it without disconnecting it.
I know that i could do this by doing dfs from one node and removing farthest vertices, but it will not really be random, it does not look good and it is not what I'm looking for.
Is there an alghoritm which can do what I want, or does anyone have some ideas to test?
edit: typical maze generation algorithms don't apply in my case, because from what I understand they work by removing edges from the graph, and here I need to remove whole vertices