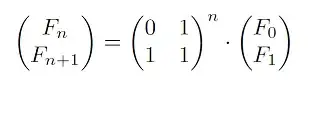big-o order of recursive and iterative fib functions?

Question

I was asked to write a fib function in the most efficient manner?

This is the implementation I provided:

public static int fib(int n)
{
    int prev1 = 1, prev2 = 1, ans = 1, i = 3;

    while (i <= n)
    {
        ans = prev1 + prev2;
        prev1 = prev2;
        prev2 = ans;
        i++;
    }
    return ans;
}

Is this the most efficient? What is the big-o order?

I was also asked to give the big-o notation of a recursive implementation:

public static int recursiveFib(int n)
{
    if (n <= 2)
        return 1;
    else
        return recursiveFib(n-1) + recursiveFib(n - 2);
}

I think this one is exponential 2^n which is why it's inefficient.

possible duplicate of [nth fibonacci number in sublinear time](http://stackoverflow.com/questions/1525521/nth-fibonacci-number-in-sublinear-time) — , May 13 '11 at 04:35

sverre · Answer 1 · 2011-05-11T01:36:19.363

8

Your implementation is O(n), and is the normal way to implement the Fibonacci function. The recursive definition is O(fib(n)) unless memoization or similar is used.

There is also a Closed form expression of the Fibonacci numbers, and This link has some implementations of faster fib functions.

edited May 11 '11 at 01:36

answered May 11 '11 at 01:27

sverre

6,768
2
27
35

1

The recursive definition can be made O(n) by returning two values. As it stands, the asymptotic performance is much worse than O(n^2), it's actually O(GoldenRatio^n). – Nathan Ryan May 11 '11 at 01:35
1

Thanks, `O(n^2)` was a misspelling, I meant to write `O(2^n)`. – sverre May 11 '11 at 01:37

score 3 · Accepted Answer · answered May 11 '11 at 05:00

I would say the best way to find fib for a particular n is using the matrix calculation method as given in Link - Page19

enter image description here

where F0 = 0 and F1 = 1. This matrix relation can easlily be used to find the fib for any value of n and n+1. The best part is that is that the multiplying matrix need not be mutliplied n times but only logN times to find the actual value of the Multiplier. Thus the overall compleixty of the algorithm is only O(logN).

The equation is derived from the basic relation of

F1 = 0*F0 + 1*F1

F1 = 1*F0 + 1*F2

Iterating over n the multiplier matrix has to be multiplied n times.

+1. For those who don't see how to cut down the number of multiplies, you can use repeated-squaring to exponentiate faster than iteration. — Andrew Lazarus, May 11 '11 at 06:23

score 2 · Answer 3 · edited May 13 '11 at 04:07

Here's the matrix method to complete this page:

public static void main(String[] args)
{
    int n = 25;
    matMul(n - 1);
    System.out.printf("\n%dth Fibonnacci number : %d\n\n", n, M[0][0]);
}

static int[][] M = {{1,0},{0,1}};
static int[][] A = {{1,1},{1,0}};
static int[][] C = {{0,0},{0,0}};

static void matMul(int n)
{
    if (n > 1)
    {
        matMul(n/2);
        mulM(0);
    }
    if (n%2!=0)
    {
        mulM(1);
    }
}

static void mulM(int m)
{
    int i,j,k;

    if (m==0)
    {
        for (i=0;i<2;i++)
            for (j=0;j<2;j++)
            {
                C[i][j]=0;
                for (k=0;k<2;k++)
                    C[i][j]+=M[i][k]*M[k][j];
            }
    }
    else
    {
        for (i=0;i<2;i++)
            for (j=0;j<2;j++)
            {
                C[i][j]=0;
                for (k=0;k<2;k++)
                    C[i][j]+=A[i][k]*M[k][j];
            }
    }
    for (i=0;i<2;i++)
            for (j=0;j<2;j++)
            {
                M[i][j]=C[i][j];
            }
}

http://www.cracktheinterview.org/2010/08/how-to-generate-fibonacci-numbers-how-to-find-out-if-a-given-number-is-a-fibonacci-number-or-not-write-c-programs-to-do-both/ — Behrooz Karjoo, May 13 '11 at 03:57

big-o order of recursive and iterative fib functions?

3 Answers3