Dear all, I am a new user of matlab on a project about dynamic system. I have two equations, in which T0, epsilon (E), a are fixed. I want to see the phage diagram when the b and c is choosen in the range in (0, 4) and (0, 100), respectively. In the graph, region I represent the unstable limit cycle while the region II the monostable and the region II the bistable region.
In fact, I think that I may be able to draw the graph by firstly arbitrarily choosing a point in b, c phage and then calculating corresponding values of x1 and x2 which enables the left part of the ODEs equals to zero. Then calculate the jacobian matrix of the right part to determine whether the egenvalue of the matrix. If it is greater than zero, then the system is unstable.
The result should be like the graph below.
But I really don't know how to determine the point on the demarcating line of the graph. Please offer your useful suggestions. Thanks in advance.
P.S: T0 = 0.1, epsilon = 0.1 a = 0.1 0 <= b <= 4.0; 0 <= c <= 100;
PP.S: The graph and equations is an excerpt from the http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2527901/ (part two: landscape and flux of biochemical oscillation network)
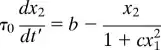

My current solution should be the following, but I cannot cat J. %Condition:
%(1) F1 = F2 = 0 (2) Jacobian = 0
%Aim:
%Obtain a non-linear equation for b and c;
a = 0.1; epslion = 0.1; T0 = 5.0;
%use the symbolic calcution
syms x y b c
F = [((epslion ^ 2 + x ^ 2 ) / ( 1 + x ^ 2) ) / (1 + y) - a * x; b / T0 - y / ( T0 * (1 + c * x ^ 2) )]; V = [x, y];
%calculate the jacobian matrix
J = jacobian(F, V);
%the symbolic solution of ODE:
%write the equation separately
S1 = dsolve ('Dx = ((epslion ^ 2 + x ^ 2 ) / ( 1 + x ^ 2) ) / (1 + y) - a * x'); S2 = dsolve ('Dy = b / T0 - y / ( T0 * (1 + c * x ^ 2) )');
BC_cal = [J(1) J(2) S1 S2]; *%%%wrong, cannot join S1, because S1 = solve(sum)****, not be calculated?*
fsolve(BC_cal);