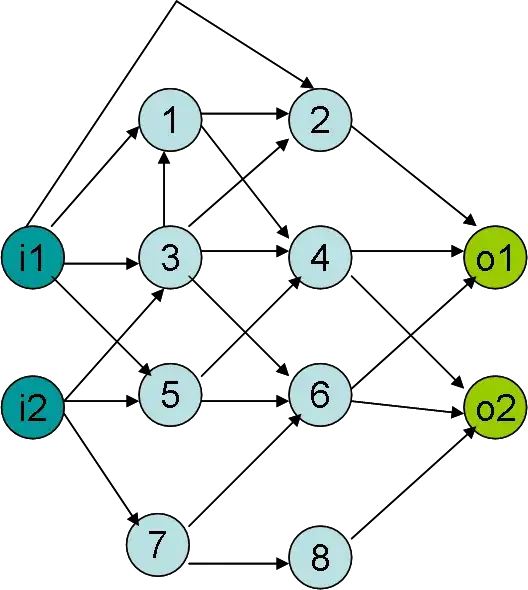
How do i find the longest path from single source to all final destinations i.e. For source i1, Give longest path between i1 -> o1 and i1 -> o2.
The legends described in the above graph are as follows: (i1, i2) are start nodes (o1, o2) are end nodes (1-8) are sub graphs The edges may have +ive/-ive weights
The longest paths in this network are in the following order:
Worst path: i1 -> 1 -> 4 -> o1
Then, all paths i1 … -> … o1
Then i1 -> 5 -> 6 -> o2
Need a way to ignore selection of (i1 -> 3) or (3 -> 4) subnetworks even though they are longer than i1 -> 5