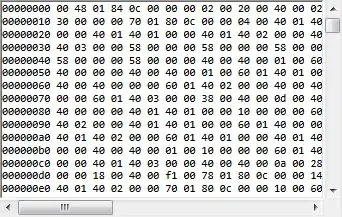
The table created shows the number (N) of rows that fall within that quartile. That is different than the wt71 values computed by summary indicating threshold for 1st or 3rd quartile or median. (Note: as @Gregor pointed out, these are quartiles not quintiles.)
To illustrate, I changed the labels to clarify the quartiles produced:
set.seed(1)
nhefs <- data.frame(
wt71 = round(runif(100, min=1, max=100), 0)
)
apply_quintiles <-function(x) {
cut(x, breaks =c(quantile(nhefs$wt71,probs=seq(0,1, by=0.25))), labels=c("0-25", "25-50", "50-75", "75-100"),include.lowest=TRUE)
}
nhefs$quintiles<-sapply(nhefs$wt71,apply_quintiles)
table(nhefs$quintiles)
0-25 25-50 50-75 75-100
25 25 26 24
This demonstrates equal distribution of the 100 random numbers across the 4 quartiles. There are N=25 between 0-25%ile and N=26 at 50-75%ile, etc. These numbers are not values of wt71 but instead of the number of data elements or rows that fall in that range of percentiles.
Here's the summary of wt71:
Min. 1st Qu. Median Mean 3rd Qu. Max.
2.00 32.75 49.50 52.24 77.00 99.00
These values correspond to thresholds for 1st quartile, median, and 3rd quartile. These threshold values do relate to value of wt71. For example, a wt71 value of 30 would be less than 1st quartile level.
Taking a look at nhefs now:
head(nhefs)
wt71 quintiles
1 27 0-25
2 38 25-50
3 58 50-75
4 91 75-100
5 21 0-25
6 90 75-100
Notice that for your different wt71 values, they are assigned to different quartiles. The wt71 of 27 is in the lowest quartile (0-25) as this value is less than the threshold for 1st quartile of 32.75.
Hope this helps!