Plotting random numbers from a given distribution along with their expected value in Python

Question

I want to compare randomly generated values sampled from certain distributions to the actual functions of those distributions.

I'm currently using matplotlib for plotting and numpy for sampling.

I found a working example for what I'm trying to achieve

# read mu, sigma, n
x = np.random.normal(mu, sigma, n)
count, bins, ignored = plt.hist(x, bins="auto", density=True)
plt.plot(bins, 1 / (sigma * np.sqrt(2 * np.pi)) * np.exp(-(bins - mu) ** 2 / (2 * sigma ** 2)), linewidth=2, color='r')
plt.show()

So x is the sample array, and they plot it using histograms, and they use the actual pdf for the function.

How would that work for the binomial distribution for instance? I followed a similar pattern:

x = np.random.binomial(N, P, n)
count, bins, ignored = plt.hist(x, bins="auto", density=True)
plt.plot(bins, scipy.special.comb(N, bins) * (P ** bins) * ((1 - P) ** (N - bins)), linewidth=2, color='r')
plt.show()

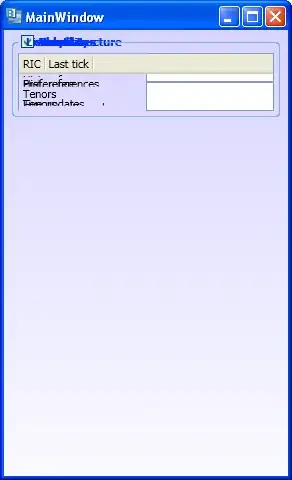
However the graph I'm getting doesn't really look right:

Well the pdf's height doesn't seem to match the histograms. What am I doing wrong? Is it the binomial function?

Answer 1

I think you got it right. Your formula for the pdf looks correct. Try it with a much larger number of samples (n) from your binomial. Recall the area under the pdf integrates to 1.0. By using the density=True your histogram is normalized as well, which is good. What happens when you don't have a large enough n? You have empty bins...and the others are relatively higher.

I ran your code for N=1000, P=0.7, n=10,000 and got a decent plot. E[X] = 700 for this. Plot looks reasonable enough...

Answer 2

The bins = "auto" defaults to the method sturges, which only accounts for data size. It is only good for gaussian data and underestimates the number of bins for large non-gaussian datasets.

Answer 3

I wasn't totally sure why you were trying to estimate the PDF based on the return parameters from the hist function, but it's possible to plot this just using scipy's binom.pmf (probability mass function, the discrete equivalent of the PDF):

N, P = 100, 0.5
f, ax1 = plt.subplots(figsize=(10, 5))
x = np.random.binomial(N, P, 50000)
count, bins, ignored = ax1.hist(x, bins="auto")
ax2 = ax1.twinx()
ax2.plot(range(100), binom.pmf(range(100), n=N, p=P))
ax2.grid(None)
plt.show()

Output:

(I hid the grid in the second ax because the two y-axes aren't quite aligned, based on this.)