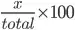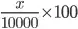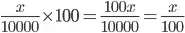Automate the boring stuff - Coin flip streaks

Question

I know there's tons of questions about it by now, even for the same problem, but I think I tried a bit of a different approach.

The task is to to 10.000 samples of 100 flips each and then compute the probability of a 6x heads or tails streak over all the samples - as far as I understand it. But in previous questions the coding problem was described as a bit fuzzy. Therefore, if you guys could just point out the errors in the code, that would be nice :)

I tried to be as lazy as possible which results in my macbook working really hard. This is my code. Do I have a problem with the first iteration of the comparison of current value to value before (as far as I understand it, I would compare index -1 (which then is index 100?) to the current one?)

import random

#variable declaration

numberOfStreaks = 0
CoinFlip = []
streak = 0

for experimentNumber in range(10000):
    # Code that creates a list of 100 'heads' or 'tails' values.
    for i in range(100):
        CoinFlip.append(random.randint(0,1))
    #does not matter if it is 0 or 1, H or T, peas or lentils. I am going to check if there is multiple 0 or 1 in a row        

    # Code that checks if there is a streak of 6 heads or tails in a row.
    for i in range(len(CoinFlip)):
        if CoinFlip[i] == CoinFlip[i-1]:  #checks if current list item is the same as before
            streak += 1 
        else:
            streak = 0

        if streak == 6:
            numberOfStreaks += 1

print('Chance of streak: %s%%' % (numberOfStreaks / 100))

Where did I make the mess? I can't really see it!

Answer 1

You need to reset the CoinFlip list. Your current program just keeps appending to CoinFlip, which makes for a very long list. This is why your performance isn't good. I also added a check for i==0 so that you're not comparing to the end of the list, because that's not technically part of the streak.

for experimentNumber in range(10000):
    # Code that creates a list of 100 'heads' or 'tails' values.
    for i in range(100):
        CoinFlip.append(random.randint(0,1))
    #does not matter if it is 0 or 1, H or T, peas or lentils. I am going to check if there is multiple 0 or 1 in a row

    # Code that checks if there is a streak of 6 heads or tails in a row.
    for i in range(len(CoinFlip)):
        if i==0:
            pass
        elif CoinFlip[i] == CoinFlip[i-1]:  #checks if current list item is the same as before
            streak += 1
        else:
            streak = 0

        if streak == 6:
            numberOfStreaks += 1

    CoinFlip = []

print('Chance of streak: %s%%' % (numberOfStreaks / (100*10000)))

I also think you need to divide by 100*10000 to get the real probability. I'm not sure why their "hint" suggest dividing by only 100.

Answer 2

I wasn't able to comment on Stuart's answer because I recently joined and don't have the reputation, so that's why this an answer on it's own. I am new to programming so anyone please correct me if I'm wrong. I was just working on the same problem in my own learning process.

First, I was unsure why you used multiple for loops when the range was the same length, so I combined those and continued to get the same results.

Also, I noticed that the final calculation is presented as a percentage but not converted to a percentage from the original calculation.

For example, 5/100 = .05 -> .05 * 100 = 5%

Therefore, I added a function that converts a decimal to percentage and rounds it to 4 decimal places.

Lastly, changed the hard coding to variables, obviously doesn't matter but just to explain the things I changed.

    import random

    #variables
    n_runs = 10000
    flips_per_run = 100
    total_instances = n_runs * flips_per_run
    coinFlip = []
    streak = 0
    numberOfStreaks = 0

    for experimentNumber in range(n_runs):
        # Code that creates a list of 100 'heads' or 'tails' values.'
        for i in range(flips_per_run):
            coinFlip.append(random.randint(0,1))
            if i==0:
                pass
            elif coinFlip[i] == coinFlip[i-1]:
                streak += 1
            else: 
                streak = 0

            if streak == 6:
                numberOfStreaks += 1

        coinFlip = []

    #calculation for chance as a decimal    
    chance = (numberOfStreaks / total_instances)
    #function that converts decimal to percent and rounds
    def to_percent(decimal):
        return round(decimal * 100,4)
    #function call to convert result
    chance_percent = to_percent(chance)
    #print result 
    print('Chance of streak: %s%%' % chance_percent)

Output: Chance of streak: 0.7834% rather than .007834%

Answer 3

I started way more complicated and now seeing your code I think that I couldn't came up with a more complicated "logic" :)

Couldn't find a working idea to write the second part!

import random

number_of_streaks = 0
coin_flips = []
streak = 0

for experiment_number in range (10000):
    # Code that creates a list of 100 'heads' and 'tails' values

def coin(coin_fl):  # Transform list into plain H or T
    for i in coin_flips[:-1]:
        print(i + ' ', end = '')

for i in range(100):    # Generates a 100 coin tosses
    if random.randint(0, 1) == 0:
        coin_head = 'H'
        coin_flips = coin_flips + [coin_head]
    else:
        coin_tail = 'T'
        coin_flips = coin_flips + [coin_tail]

coin(coin_flips)

Answer 4

import random
numStreaks = 0
test = 0
flip = []

#running the experiment 10000 times

for exp in range(10000):
    for i in range(100): #list of 100 random heads/tails

        if random.randint(0,1) == 0:
            flip.append('H')
        else:
            flip.append('T')

    for j in range(100): #checking for streaks of 6 heads/tails

        if flip[j:j+6] == ['H','H','H','H','H','H']:
            numStreaks += 1
        elif flip[j:j+6] == ['T','T','T','T','T','T']:
            numStreaks += 1
        else:
            test += 1 #just to test the prog
            continue
print (test)
chance = numStreaks / 10000
print("chance of streaks of 6: %s %%" % chance )

Answer 5

The following is a set of minor modifications to the initially provided code that will compute the estimate correctly.

I have marked modifications with comments prefixed by #### and numbered them with reference to the explanations that follow.

import random

#variable declaration

numberOfStreaks = 0

for experimentNumber in range(10000):
    # Code that creates a list of 100 'heads' or 'tails' values.
    CoinFlip = [] #### (1) create a new, empty list for this list of 100
    for i in range(100):
        CoinFlip.append(random.randint(0,1))
    #does not matter if it is 0 or 1, H or T, peas or lentils. I am going to check if there is multiple 0 or 1 in a row        

    #### # (6) example / test
    #### # if uncommented should be 100%
    #### CoinFlip = [ 'H', 'H', 'H', 'H', 'H', 'H', 'T', 'T', 'T', 'T', 'T', 'T' ]

    # Code that checks if there is a streak of 6 heads or tails in a row.
    streak = 1 #### (2, 4) any flip is a streak of (at least) 1; reset for next check
    for i in range(1, len(CoinFlip)): #### (3) start at the second flip, as we will look back 1
        if CoinFlip[i] == CoinFlip[i-1]:  #checks if current list item is the same as before
            streak += 1
        else:
            streak = 1 #### (2) any flip is a streak of (at least) 1

        if streak == 6:
            numberOfStreaks += 1
            break #### (5) we've found a streak in this CoinFlip list, skip to next experiment
                  #### if we don't, we get percentages above 100, e.g. the example / test above
                  #### this makes some sense, but is likely not what the book's author intends

print('Chance of streak: %s%%' % (numberOfStreaks / 100.0))

Explanation of these changes

The following is a brief explanation of these changes. Each is largely independent, fixing a different issue with the code.

1. the clearing/creating of the CoinFlip list at the start of each experiment
   • without this the new elements are added on to the list from the previous experiment
2. the acknowledgement that any flip, even a single 'H' or 'T' (or 1 or 0), represents a streak of 1
   • without this change the code actually requires six subsequent matches to the initial coin flip, for a total streak of seven (a slightly less intuitive alternative change would be to replace if streak == 6: with if streak == 5:)
3. starting the check from the second flip, using range(1, len(CoinFlip)) (n.b. lists are zero-indexed)
   • as the code looks back along the list, a for loop with a range() starting with 0 would incorrectly compare index 0 to index -1 (the last element of the list)
4. (moving the scope and) resetting the streak counter before each check
   • without this change an initial streak in an experiment could get added to a partial streak from a previous experiment (see Testing the code for a suggested demonstration)
5. exiting the check once we have found a streak
   • "the second part checks if there is a streak in it" - Coin Flip Streaks

This question in the book is somewhat poorly specified, and final part could be interpreted to mean any of "check if [at least?] a [single?] streak of [precisely?] six [or more?] is found". This solution interprets check as a boolean assessment (i.e. we only record that this list contained a streak or that it did not), and interprets a non-exclusively (i.e. we allow longer streaks or multiple streaks to count; as was true in the code provided in the question).

(Optional 6.) Testing the code

The commented out "example / test" allows you to switch out the normally randomly generated flips to the same known value in every experiment. In this case a fixed list that should calculate as 100%. If you disagree with interpretation of the task specification and disable the exit of the check described in (5.), you might expect the program to report 200% as there are two distinct streaks of six in every experiment. Disabling the break in combination with this input reports precisely that.

You should always use this type of technique (use known input, verify output) to convince yourself that code does or does not work as it claims or as you expect.

The fixed input CoinFlip = [ 'H', 'H', 'H', 'H', 'T', 'T', 'T' ] can be used to highlight the issue fixed by (4.). If reverted, the code would calculate the percentage of experiments (all with this input) containing a streak of six consecutive H or T as 50%. While (5.) fixes an independent issue, removing the break that was added further exacerbates the error and raises the calculated percentage to 99.99%. For this input, the calculated percentage containing a streak of six should be 0%.

You'll find the complete code, as provided here, produces estimates of around 80%. This might be surprising, but the author of the book hints that this might be the case:

A human will almost never write down a streak of six heads or six tails in a row, even though it is highly likely to happen in truly random coin flips.

- Al Sweigart, Coin Flip Streaks

You can also consider additional sources. WolframAlpha calculates that the chance of getting a "streak of 6 heads in 100 coin flips" is approximately 1 in 2. Here we are estimating the chance of getting a streak of 6 (or more) heads or a streak of six (or more) tails, which you can expect to be even more likely. As a simpler, independent example of this cumulative effect: consider that the chance of picking a heart from a normal pack of playing cards is 13 in 52, but picking a heart or a diamond would be 26 in 52.

---

Notes on the calculation

It may also help to understand that the author also takes a shortcut with calculating the percentage. This may confuses beginners looking at the final calculation.

Recall, a percentage is calculated:

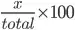
We know that total number of experiments to run will be 10000

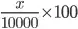
Therefore

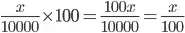
Postscript: I've taken the liberty of changing 100 to 100.0 in the final line. This allows the code to calculate the percentage correctly in Python 2. This is not required for Python 3, as specified in the question and book.

Answer 6

My amateur attempt

import random

#reset strakes
numberOfStreaks = 0
#main loop
for experimentNumber in range(10000):

    # Code that creates a list of 100 'heads' or 'tails' values.
    # assure the list is empty and all counters are 0
    coinFlip=[]
    H=0
    T=0
    for fata in range(100):
        # generate random numbers for head / tails
        fata = random.randint(0,1)
        #if head, append 1 head and reset counter for tail
        if fata == 0:
            coinFlip.append('H')
            H += 1
            T = 0
        #else if tail append 1 tail and reset counter for head
        elif fata == 1:
            coinFlip.append('T')
            T += 1
            H = 0

    # Code that checks if there is a streak of 6 heads or tails in a row.
    # when head and tail higher than 6 extract floored quotient and append it to numberOfStreaks,
    # this should take into consideration multiple streaks in a row.

    if H > 5 or T > 5:
        numberOfStreaks += (H // 6) or (T // 6) 

print('Chance of streak: %s%%' % (numberOfStreaks / 100))

Output:

Chance of streak: 3.18%

Answer 7

This code seams to give correct probability of around 54% as checked on wolfram alpha in a previous post above

import random
numberOfStreaks = 0

for experimentNumber in range(10000):
    # Code that creates a list of 100 'heads' or 'tails' values.
    hundredList = []
    streak = 0
    for i in range(100):
        hundredList.append(random.choice(['H','T']))
    # Code that checks if there is a streak of 6 heads or tails in a row.
    for i in range(len(hundredList)):
        if i == 0:
            pass
        elif hundredList[i] == hundredList[(i-1)]:
            streak += 1
        else:
            streak = 0

        if streak == 6:
            numberOfStreaks += 1
            break
        
print('Chance of streak: %s%%' % (numberOfStreaks / 100))

Answer 8

I think all the answers add something to the question!!! brilliant!!! But, shouldn't it be 'streak == 5' if we are looking for 6 continuous same coin flip. For ex, THHHHHHT, streak == 6 won't be helpful here.

Code for just 100 flips:

coinFlipList = []

for i in range(0,100):
    if random.randint(0,1)==0:
        coinFlipList.append('H')
    else:
        coinFlipList.append('T')
print(coinFlipList)

totalStreak = 0
countStreak = 0
for index,item in enumerate(coinFlipList):
    if index == 0:
        pass
    elif coinFlipList[index] == coinFlipList[index-1]:
        countStreak += 1
    else:
        countStreak = 0
    if countStreak == 5:
        totalStreak += 1
print('Total streaks %s' %(totalStreak))

Let me know, if I missed anything.

Answer 9

Here is what im doing

import random
numberOfStreaks = 0
totalFor10000Times = []
for experimentNumber in range(10000):
    listOfflips = []
    for flipsTime in range(100):
        if random.randint(0,1) == 0:
            listOfflips.append('H')
        else:
            listOfflips.append('T')
    totalFor10000Times.append(listOfflips)

    for y in range(100):
        if listOfflips[y:y+6] == ['T','T','T','T','T','T']:
            numberOfStreaks += 1
        elif listOfflips[y:y+6] == ['H','H','H','H','H','H']:
            numberOfStreaks += 1
        else:
            pass
print(numberOfStreaks)
#percent = (x/total)*100
#but here you can see the numberOfStreaks contains 6 elements of each list so to 
#find out the total elements contained by the numberOfStreaks, we will need to 
#multiply numberOfStreaks by 6 or devide 1000000 (a million) by 6 (for this, 
#because we put 100 times of flip (each flip returns 100 elements) in 1 
#experiment count, so to see how many times of flip does 10000 experiment count 
#contains, we need to multiply it with 100 (10000 * 100 = 1000000), and that's 
#the 'total')
print('Chance of streak: %s%%' % round((numberOfStreaks / (1000000/6))*100,2))

Answer 10

The book code is wrong when it says to divide the result by 100. You must divide by 10,000.

import random

numberOfStreaks = 0
for experimentNumber in range(10000):
    # Code that creates a list of 100 'heads' or 'tails' values.
    flips = []
    for i in range(100):
        flips.append(random.randint(0, 1))

    # Code that checks if there is a streak of 6 heads or tails in a row.
    count = 1
    for i in range(1, len(flips)):
        if flips[i] == flips[i - 1]:
            count += 1
        else:
            count = 1

        if count % 6 == 0:
            numberOfStreaks += 1

print('Chance of streak (SIMULATION): %s%%' % (numberOfStreaks / 10000))
print('Chance of streak (MATH): %s%%' % ((1/2)**6 * 100))

Answer 11

I'm Al Sweigart, author of Automate the Boring Stuff and author of this original problem. I'm afraid I made this inadvertently too difficult (there were even some issues I didn't foresee when I wrote it.)

First of all, we need to know that in a series of 100 coin flips, there's about an 80% chance that it will contain 6 heads or 6 tails in a row. I won't point out the math, because people will argue and say my math is wrong. Instead, let's do this empirically.

Let's generate 10,000 series of 100 coin flips as strings of "H" and "T":

import random
for experimentNumber in range(10000):
    # Code that creates a list of 100 'heads' or 'tails' values.
    flips = []
    for i in range(100):
        if random.randint(0,1):
            flips.append('H')
        else:
            flips.append('T')

    print(''.join(flips))

This produces 10,000 lines of output, where each line looks like this:

HHHTTTTTHTTHTHHHTHTHTHTHHHTTTHHTHTHTTHHHTHHHTHTTHHHTTHTHHTHHTTHTTTTHTHHHHTHHTHHTHHTHTHTHTHHTHHHHHTHH

Copy and paste the full output into a text editor and verify that there are 10,000 lines. Next, let's find out how many have streaks of 6 heads or tails. A streak will appear as "HHHHHH" or "TTTTTT", so let's do a regex find-and-replace to find ^.*HHHHHH.*$ and replace it with an empty string. This blanks out all the lines that contain "HHHHHH" somewhere on the line. Then do the same with ^.*TTTTTT.*$

What's left are the lines that do NOT contain a 6-streak. You can verify this by searching for "HHHHHH" and "TTTTTT" and not finding any instances. There's a bunch of blank lines, so let's get rid of them all by repeatedly replacing \n\n with \n. Then count how many lines you have.

On my run (it's random for everyone, but your results should be roughly the same), I had 1903 lines left in the text file. This means that 10000 - 1903 = 8097 lines had a streak of 6 or more.

8,097 out of 10,000 is 80.97%. You can calculate this by doing 8097 / 10000 * 100, which is equivalent to 8097 / 100. (Some folks thought the template code dividing by 100 was wrong, but it's not.)

Here's my complete solution:

import random
numberOfStreaks = 0
for experimentNumber in range(10000):
    # Code that creates a list of 100 'heads' or 'tails' values.
    flips = []
    for i in range(100):
        if random.randint(0,1):
            flips.append('H')
        else:
            flips.append('T')

    # Code that checks if there is a streak of 6 heads or tails in a row.
    for i in range(100 - 6):
        if flips[i] == flips[i+1] == flips[i+2] == flips[i+3] == flips[i+4] == flips[i+5]:
            numberOfStreaks += 1
            break

print('Chance of streak: %s%%' % (numberOfStreaks / 100))

This produces the output:

Chance of streak: 80.56%

Now, what's tricky about this is that you need to make sure you don't double count two 6+ streaks in the same experimental sample. So if a sample contains HTHTHHHHHHTHTHHHHHH it should only count once even though there are two streaks. It's also easy to make an off-by-one error because remember that an H or T by itself is a streak of length 1, not of length 0.

So to fix the original program, it should look like this:

import random

#variable declaration

numberOfStreaks = 0

for experimentNumber in range(10000):
    # Code that creates a list of 100 'heads' or 'tails' values.
    CoinFlip = [] # CHANGE: Reset the list for each sample.
    for i in range(100):
        CoinFlip.append(random.randint(0,1))
    #does not matter if it is 0 or 1, H or T, peas or lentils. I am going to check if there is multiple 0 or 1 in a row        

    # Code that checks if there is a streak of 6 heads or tails in a row.
    streak = 1 # CHANGE: Streaks start at 1
    for i in range(1, len(CoinFlip)):  # CHANGE: Start at index 1, since you are looking at the previous one.
        if CoinFlip[i] == CoinFlip[i-1]:  #checks if current list item is the same as before
            streak += 1 
        else:
            streak = 1

        if streak == 6:
            numberOfStreaks += 1
            break  # CHANGE: Break after finding one 6-streak, since you don't want to double count in the same series of 100-flips.

print('Chance of streak: %s%%' % (numberOfStreaks / 100))

You should note that getting six similar flips in a row is almost certainly going to happen in a series of 100 coin flips, hence the (perhaps surprising) high number of 80%.