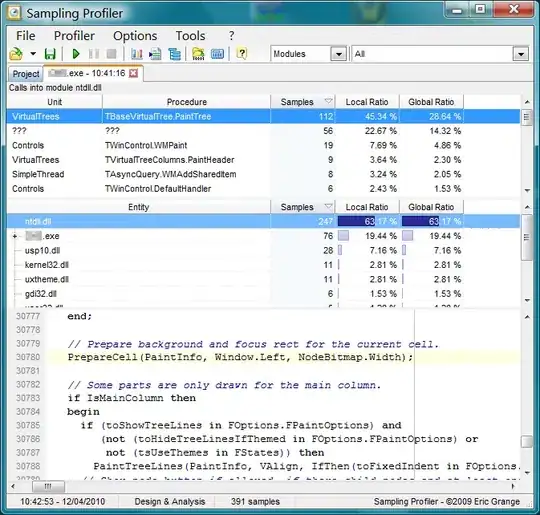
I want to estimate multiplicity of polynomial roots.
I have found some info about it, choosed the test example and made c program
Here should be 4 roots. One simple root and one with multiplicity 3.
#include <complex.h>
#include <math.h>
#include <stdio.h>
complex long double z0 = +1.5; // exact period = 1 stability = 3.000000000000000000 multiplicity = ?
complex long double z1 = -0.5; // exact period = 2 stability = 0.999999999999900080 multiplicity = ?
complex long double c = -0.75; // parameter of the f function
/*
https://en.wikibooks.org/wiki/Fractals/Mathematics/Newton_method
*/
int GiveMultiplicity(const complex long double c, const complex long double z0 , const int pMax){
complex long double z = z0;
complex long double d = 1.0; /* d = first derivative with respect to z */
complex long double e = 0.0; // second derivative with respect to z
complex long double m;
int multiplicity;
int p;
for (p=0; p < pMax; p++){
d = 2*z*d; // f' = first derivative with respect to z */
e = 2*(d*d +z*e); // f'' = second derivative with respect to z
z = z*z +c ; // f = complex quadratic polynomial
}
m = (d*d)/(d*d -z*e);
multiplicity = (int) round(cabs(m));
return multiplicity;
}
int main(){
int m;
m = GiveMultiplicity(c, z0, 1);
printf("m = %d \n", m);
m = GiveMultiplicity(c, z1, 1);
printf("m = %d \n", m);
m = GiveMultiplicity(c, z1, 2);
printf("m = %d \n", m);
return 0;
}
The result is :
m=1
m=1
m=1
Is it good ? Maybe I should simply add the results ?
Good results using symbolic computations are roots: [ 3/2, -1/2] and its multiplicities : [1,3]
Here is a graph of the function f(z)= (z^2-0.75)^2-z-0.75 = z^4-1.5*z^2-z-3/16

Is it possibly to compute the similar values numerically ?