I've been searching far and wide on the seven internets, and have come to no avail. The closest to what I need seems to be The cutting stock problem, only in 2D (which is disappointing since Wikipedia doesn't provide any directions on how to solve that one). Another look-alike problem would be UV unwrapping. There are solutions there, but only those that you get from add-ons on various 3D software.
Cutting the long talk short - what I want is this: given a rectangle of known width and height, I have to find out how many shapes (polygons) of known sizes (which may be rotated at will) may I fit inside that rectangle.
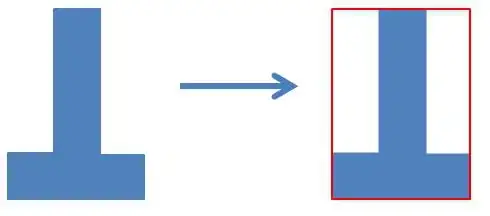
For example, I could choose a T-shaped piece and in the same rectangle I could pack it both in an efficient way, resulting in 4 shapes per rectangle

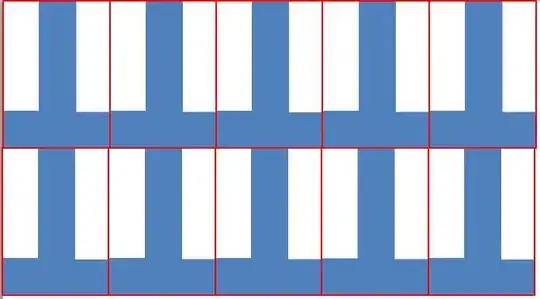
as well as tiling them based on their bounding boxes, case in which I could only fit 3
But of course, this is only an example... and I don't think it would be much use to solving on this particular case. The only approaches I can think of right now are either like backtracking in their complexity or solve only particular cases of this problem. So... any ideas?