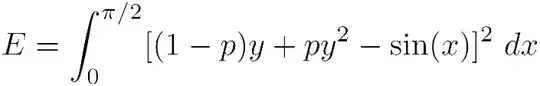sin and cos are slow, is there an alternatve?

Question

My game needs to move by a certain angle. To do this I get the vector of the angle via sin and cos. Unfortunately sin and cos are my bottleneck. I'm sure I do not need this much precision. Is there an alternative to a C sin & cos and look-up table that is decently precise but very fast?

I had found this:

float Skeleton::fastSin( float x )
{
    const float B = 4.0f/pi;
    const float C = -4.0f/(pi*pi);

    float y = B * x + C * x * abs(x);

    const float P = 0.225f;

    return P * (y * abs(y) - y) + y; 
}

Unfortunately, this does not seem to work. I get significantly different behavior when I use this sin rather than C sin.

Thanks

Answer 1

A lookup table is the standard solution. You could Also use two lookup tables on for degrees and one for tenths of degrees and utilize sin(A + B) = sin(a)cos(b) + cos(A)sin(b)

Answer 2

For your fastSin(), you should check its documentation to see what range it's valid on. The units you're using for your game could be too big or too small and scaling them to fit within that function's expected range could make it work better.

EDIT:

Someone else mentioned getting it into the desired range by subtracting PI, but apparently there's a function called fmod for doing modulus division on floats/doubles, so this should do it:

#include <iostream>
#include <cmath>

float fastSin( float x ){
    x = fmod(x + M_PI, M_PI * 2) - M_PI; // restrict x so that -M_PI < x < M_PI
    const float B = 4.0f/M_PI;
    const float C = -4.0f/(M_PI*M_PI);

    float y = B * x + C * x * std::abs(x);

    const float P = 0.225f;

    return P * (y * std::abs(y) - y) + y; 
}

int main() {
    std::cout << fastSin(100.0) << '\n' << std::sin(100.0) << std::endl;
}

I have no idea how expensive fmod is though, so I'm going to try a quick benchmark next.

Benchmark Results

I compiled this with -O2 and ran the result with the Unix time program:

int main() {
    float a = 0;
    for(int i = 0; i < REPETITIONS; i++) {
        a += sin(i); // or fastSin(i);
    }
    std::cout << a << std::endl;
}

The result is that sin is about 1.8x slower (if fastSin takes 5 seconds, sin takes 9). The accuracy also seemed to be pretty good.

If you chose to go this route, make sure to compile with optimization on (-O2 in gcc).

Answer 3

I know this is already an old topic, but for people who have the same question, here is a tip.

A lot of times in 2D and 3D rotation, all vectors are rotated with a fixed angle. In stead of calling the cos() or sin() every cycle of the loop, create variable before the loop which contains the value of cos(angle) or sin(angle) already. You can use this variable in your loop. This way the function only has to be called once.

Answer 4

If you rephrase the return in fastSin as

return (1-P) * y + P * (y * abs(y))

And rewrite y as (for x>0 )

y = 4 * x * (pi-x) / (pi * pi)

you can see that y is a parabolic first-order approximation to sin(x) chosen so that it passes through (0,0), (pi/2,1) and (pi,0), and is symmetrical about x=pi/2. Thus we can only expect our function to be a good approximation from 0 to pi. If we want values outside that range we can use the 2-pi periodicity of sin(x) and that sin(x+pi) = -sin(x).

The y*abs(y) is a "correction term" which also passes through those three points. (I'm not sure why y*abs(y) is used rather than just y*y since y is positive in the 0-pi range).

This form of overall approximation function guarantees that a linear blend of the two functions y and y*y, (1-P)*y + P * y*y will also pass through (0,0), (pi/2,1) and (pi,0).

We might expect y to be a decent approximation to sin(x), but the hope is that by picking a good value for P we get a better approximation.

One question is "How was P chosen?". Personally, I'd chose the P that produced the least RMS error over the 0,pi/2 interval. (I'm not sure that's how this P was chosen though)

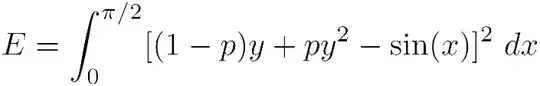
Minimizing this wrt. P gives

This can be rearranged and solved for p

Wolfram alpha evaluates the initial integral to be the quadratic

E = (16 π^5 p^2 - (96 π^5 + 100800 π^2 - 967680)p + 651 π^5 - 20160 π^2)/(1260 π^4)

which has a minimum of

min(E) = -11612160/π^9 + 2419200/π^7 - 126000/π^5 - 2304/π^4 + 224/π^2 + (169 π)/420 
       ≈ 5.582129689596371e-07

at

p = 3 + 30240/π^5 - 3150/π^3 
  ≈ 0.2248391013559825

Which is pretty close to the specified P=0.225.

You can raise the accuracy of the approximation by adding an additional correction term. giving a form something like return (1-a-b)*y + a y * abs(y) + b y * y * abs(y). I would find a and b by in the same way as above, this time giving a system of two linear equations in a and b to solve, rather than a single equation in p. I'm not going to do the derivation as it is tedious and the conversion to latex images is painful... ;)

NOTE: When answering another question I thought of another valid choice for P. The problem is that using reflection to extend the curve into (-pi,0) leaves a kink in the curve at x=0. However, I suspect we can choose P such that the kink becomes smooth. To do this take the left and right derivatives at x=0 and ensure they are equal. This gives an equation for P.

Answer 5

You can compute a table S of 256 values, from sin(0) to sin(2 * pi). Then, to pick sin(x), bring back x in [0, 2 * pi], you can pick 2 values S[a], S[b] from the table, such as a < x < b. From this, linear interpolation, and you should have a fair approximation

• memory saving trick : you actually need to store only from [0, pi / 2], and use symmetries of sin(x)
• enhancement trick : linear interpolation can be a problem because of non-smooth derivatives, humans eyes is good at spotting such glitches in animation and graphics. Use cubic interpolation then.

Answer 6

What about

x*(0.0174532925199433-8.650935142277599*10^-7*x^2)

for deg and

x*(1-0.162716259904269*x^2)

for rad on -45, 45 and -pi/4 , pi/4 respectively?

Answer 7

you can use this aproximation.

this solution use a quadratic curve :

http://www.starming.com/index.php?action=plugin&v=wave&ajax=iframe&iframe=fullviewonepost&mid=56&tid=4825

Answer 8

This (i.e. the fastsin function) is approximating the sine function using a parabola. I suspect it's only good for values between -π and +π. Fortunately, you can keep adding or subtracting 2π until you get into this range. (Edited to specify what is approximating the sine function using a parabola.)