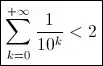plotting 3D surface with plotly (matrix transformation with akima::interp)

Question

In order to plot a surface in plotly with x, y, z, we can use the function interp to create the data (as input for the add_surface function in plotly)

This article give the solution.

I follow the different steps. With the follow code, we can plotly a surface with markers.

library(akima)
library(plotly)

x=rep(seq(-1,5,0.2),time=31,each=1)
y=rep(seq(-1,5,0.2),time=1,each=31)

df=data.frame(x=x,y=y,
              z=2*x+y-1.4)


fig <- plot_ly()%>% add_markers(data=df,x = ~x, y = ~y, z = ~z,
          marker = list(color = "blue",
                        showscale = TRUE))

fig

We can see the following plot

Then I use interp to create the data for the surface, and I plot the surface together with the markers.

s = interp(x = df$x, y = df$y, z = df$z)

fig <- plot_ly()%>% 
  add_surface(x = s$x, y = s$y, z = s$z)%>%
  add_markers(data=df,x = ~x, y = ~y, z = ~z,
              marker = list(color = "blue",
                            showscale = TRUE))

fig

I have the following image.

We can see that the result is different. And I can't see why.

When I try to change the function to generate z, sometimes, the two surfaces are the same. For example, for this data.frame

df=data.frame(x=x,y=y,
              z=x+y+1)

We have the following image. And we can see that this time, we get the same surfaces.

Answer 1

It appears the meanings of x and y are swapped in the add_surface versus the meanings in interp. The example that worked had x and y appear symmetrically. So swap them back by transposing the z matrix:

fig <- plot_ly()%>% 
  add_surface(x = s$x, y = s$y, z = t(s$z))%>%
  add_markers(data=df,x = ~x, y = ~y, z = ~z,
              marker = list(color = "blue",
                            showscale = TRUE))

fig

This is just a guess because the documentation in plotly is so weak. akima::interp clearly documents that rows of z correspond to different x values.