This has been racking my brain for hours now. I will try to explain as much as I can. I'm aware this code is horrendously ungraceful, but I'm new to Fortran and making things more efficient is not easy for me.
I am trying to simulate the celestial motion I've specified in the title. I am going to have (before moving to the co-moving frame) the Sun at the origin of coordinates, the Earth at x = 149597870d+3meters away (the mean distance from the Sun to the Earth I believe), y = 0. For the moon, I'm having it at the distance from the Moon to Earth (384400d+3 meters) plus the distance from the Earth to the Sun, so that we essentially have a situation where all planets are situated on the y = 0 line, with the Earth an astronomical unit away in the x-axis, and the moon a further distance away equal to the distance between the Earth and the moon.
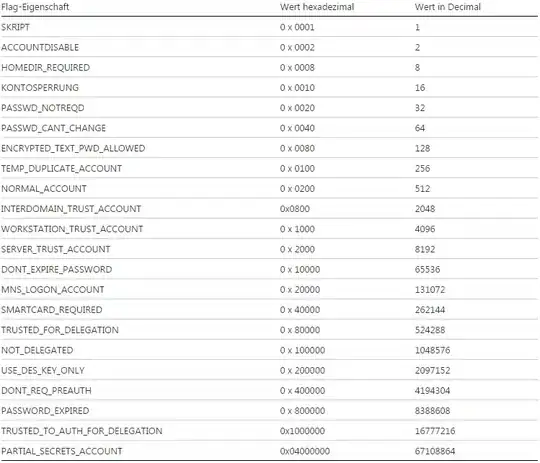
I've attempted to illustrate the situation, as well as the free body diagrams, in the following two images.
From there, I've defined a 12 dimensional array, sol, which holds the x and y positions and velocities of each body such that sol = (x1,y1,x2,y2,x3,y3,dx1/dt,dy1/dt,dx2/dt,dy2/dt,dx3/dt,dy3/dt). I then initialized the array: the sun will have no initial velocities, the Earth will have an initial y velocity equal to its mean orbital velocity around the sun with no initial x velocity, and the moon will have an initial y velocity equal to its mean orbital velocity around the earth and no initial x velocity.
inits(1:2) = 0d0
inits(3) = distE
inits(4) = 0d0
inits(5) = distE+distM
inits(6:9) = 0d0
inits(10) = vE
inits(11) = 0d0
inits(12) = vM
sol = inits
I then attempt to bring everything to a co-moving frame based off the following equation:
mf = 0
Mtot = mSun + mEarth + mMoon
mf(1:2) = mSun/(Mtot) * mf(1:2) + mEarth/(Mtot) * sol(3:4) + mMoon/(Mtot) * sol(5:6)
mf(3:4) = mEarth/(Mtot) * mf(3:4) + mSun/(Mtot) * sol(1:2) + mMoon/(Mtot) * sol(5:6)
mf(5:6) = mMoon/(Mtot) * mf(5:6) + mSun/(Mtot) * sol(1:2) + mEarth/(Mtot) * sol(3:4)
mf(7:8) = mSun/(Mtot) * mf(7:8) + mEarth/(Mtot) * sol(9:10) + mMoon/(Mtot) * sol(11:12)
mf(9:10) = mEarth/(Mtot) * mf(9:10) + mSun/(Mtot) * sol(7:8) + mMoon/(Mtot) * sol(11:12)
mf(11:12) = mMoon/(Mtot) * mf(11:12) + mSun/(Mtot) * sol(7:8) + mEarth/(Mtot) * sol(9:10)
sol = inits - mf
I then use a varied timestep for my calculations based off the equation:
real*8 function fun_tstepq8(arr)
use importants
implicit none
real*8,dimension(12), intent(in) :: arr
real*8::alp,part1,part2,part3,distEtoS,distEtoM,distStoM
real*8 :: distEdottoMdot,distEdottoSdot,distSdottoMdot
alp = 1d-4
distEtoS = SQRT((sol(3)-sol(1))**2 + (sol(4)-sol(2))**2)**3
distEtoM = SQRT((sol(5)-sol(3))**2 + (sol(6)-sol(4))**2)**3
distStoM = SQRT((sol(5)-sol(1))**2 + (sol(6)-sol(2))**2)**3
distEdottoSdot = SQRT((sol(9)-sol(7))**2 + (sol(10)-sol(8))**2)
distEdottoMdot = SQRT((sol(11)-sol(9))**2 + (sol(12)-sol(10))**2)
distSdottoMdot = SQRT((sol(11)-sol(7))**2 + (sol(12)-sol(8))**2)
part1= distEtoS/distEdottoSdot
part2= distEtoM/distEdottoMdot
part3= distStoM/distSdottoMdot
fun_tstepq8 = alp * MIN(part1,part2,part3)
end function
Putting that all together, I use a Forward Euler method and calculate the function f from y0 = y0 + hf using the subroutine:
subroutine q8RHS(sol)
use importants, ONLY: mSun, mEarth,mMoon, F, G
implicit none
real*8 :: distEtoS,distEtoM,distStoM
real*8,dimension(12) :: sol
integer :: i
distEtoS = SQRT((sol(3)-sol(1))**2 + (sol(4)-sol(2))**2)**3
distEtoM = SQRT((sol(5)-sol(3))**2 + (sol(6)-sol(4))**2)**3
distStoM = SQRT((sol(5)-sol(1))**2 + (sol(6)-sol(2))**2)**3
do i = 1,12
if (i < 7) then
F(i) = sol(i+6)
elseif (i < 9) then
F(i) = G * (mEarth * (sol(i-4) - sol(i-6))/distEtoS + mMoon * (sol(i-2) - sol(i-6))/distStoM)
elseif (i < 11) then
F(i) = G * mSun * (sol(i-6) - sol(i-8))/distEtoS - mMoon * G *(sol(i-4) - sol(i-6))/distEtoM
else
F(i) = -G * mSun * (sol(i-6) - sol(i-10))/distStoM -G*mEarth * (sol(i-6) - sol(i-8))/distEtoM
endif
enddo
end subroutine
In terms of deriving the q8RHS subroutine, I started with:
And then this is my work to derive mechanics for one of the planets. Note I use the Euler method here, and derive suitable functions to use for f(x,t) = dx/dt form needed for the Euler method. Note I couldn't use the denominator I derived as at some point x2 = x1 in my simulation if I use this, hence the issue I talked about with the timestep getting tiny enough where the simulation grinds to a halt.
Overall, my program looks like this:
module importants
implicit none
integer,parameter::Ndim = 3
integer:: N,N2
real*8, parameter :: G = 6.67408e-11
integer,parameter :: Nbodies = 2
integer::specific_Nbodies = 2*Nbodies
real*8,dimension(12) :: inits,sol,F
real*8 :: d_j = 778.547200d+9
real*8 :: v_j = 13.1d+3
integer :: rank = Nbodies * Ndim * 2
real*8 :: mSun = 1.989d+30
real*8, dimension(12) :: mf
real*8 :: mJup = 1.89819d+27
real*8, parameter :: pi= DACOS(-1.d0)
real*8 :: a,P,FF
real*8 :: pJ = 374080032d0
real*8, dimension(2) :: QEcompare,QLcompare,QPcompare
real*8 :: mEarth = 5.9722d+24
real*8 :: mMoon = 7.34767309d+22
real*8 :: distE = 149597870d+3 ! Dist from sun to earth
real*8 :: distM = 384400d+3 ! Dist from earth to moon
real*8 :: distMS = 152d+9
real*8 :: vE = 29.78d+3
real*8 :: vM = 1.022d+3
end module
program exercise3
use importants
implicit none
print*,'two'
!call solve()
!call q3()
!call q4()
!call q5()
!call q5circ()
!call q6ecc()
!call q6pt2()
!call q7()
call q8()
end program
subroutine q8()
use importants
implicit none
!real*8,external :: Epot,Ekin, L
real*8,external :: fun_tstepq8
real*8 :: tstep,time,tracker,Mtot,t
!real*8,dimension(2) :: Etot,L1,L2
!real*8, dimension(3,2) :: r2
integer :: j,i
print*, 'Starting Q8. -------------------------------------------------------'
inits(1:2) = 0d0
inits(3) = distE
inits(4) = 0d0
inits(5) = distE+distM
inits(6:9) = 0d0
inits(10) = vE
inits(11) = 0d0
inits(12) = vM
sol = inits
mf = 0
Mtot = mSun + mEarth + mMoon
mf(1:2) = mSun/(Mtot) * mf(1:2) + mEarth/(Mtot) * sol(3:4) + mMoon/(Mtot) * sol(5:6)
mf(3:4) = mEarth/(Mtot) * mf(3:4) + mSun/(Mtot) * sol(1:2) + mMoon/(Mtot) * sol(5:6)
mf(5:6) = mMoon/(Mtot) * mf(5:6) + mSun/(Mtot) * sol(1:2) + mEarth/(Mtot) * sol(3:4)
mf(7:8) = mSun/(Mtot) * mf(7:8) + mEarth/(Mtot) * sol(9:10) + mMoon/(Mtot) * sol(11:12)
mf(9:10) = mEarth/(Mtot) * mf(9:10) + mSun/(Mtot) * sol(7:8) + mMoon/(Mtot) * sol(11:12)
mf(11:12) = mMoon/(Mtot) * mf(11:12) + mSun/(Mtot) * sol(7:8) + mEarth/(Mtot) * sol(9:10)
sol = inits - mf
print*, '---------------------------------------------------------------------'
print*, 'Beginning fixed t timestep. '
t = 0d0
P = 3.154d+7
time=0
tracker=0
print*, 'P understood as :', P
open(70,file='q8.dat')
time=0
tracker=0
write(70,*) sol(1),sol(2),sol(3),sol(4),sol(5),sol(6)
do while(time.le.P)
call q8RHS(sol)
tstep=fun_tstepq8(sol)
time=time+tstep
tracker=tracker+1
print*, tstep
do i=1,12
sol(i) = sol(i) + tstep * F(i)
enddo
write(70,*) sol(1),sol(2),sol(3),sol(4),sol(5),sol(6)
enddo
end subroutine
I know there are a bunch of variables that are not used here, but were used for other subroutines, as this is a bit, ungainly beast of a program I've made. I just know that the previous subroutines and all of their related variables have run fine, and I have no issue with them and they don't interfere with the code I have in mind.
Anyway, once I run the program, the time step is immediately made massive, and then the program completes in an iteration or two, as the denominators in my time step function has its denominators become tiny very quickly. Before showing the code I have here, I initially noticed that the Earth and Moon don't interact and the Moon just barrels towards the sun while the Earth orbits the Sun normally. It looked like this (note that this is with a different RHS subroutine, not the one I listed, but just for context):
I tried to then initially look at the Earth and Moon itself with a fixed time step. I eventually got them to "see eachother" (interact with their gravitational fields in a way that made sense) but as soon as the Moon got close to the Earth it slingshotted back away from it (I think as soon as it went just past the Earth so that it was just barely closer to the Sun than the Earth was) and just kept shooting away. I tried using a varied timestep, but it then had such a small timestep everything slowed down to a half once the Moon got close enough to the Earth. This was using a timestep equation that only considered the x positions of the Moon and Earth. I then tried adjusting the timestep so that it looks like how I've listed it by staring at the equation I've pictured longer, which caused the massive timesteps I've discussed. I then gave up, and brought back the Sun's presence which is the code I've listed here. I'm absolutely stumped. Here's how the trajectories look with the code I have now:
What is wrong with my code? What aren't I simulating the orbit properly? What am I doing wrong?
UPDATE
On the advice of one of the commentors, I made alp smaller. Here is the result:
and a more zoomed in version.
The Earth gets outright repelled, and the moon is flung towards the Sun.
UPDATE 2
I believe I corrected a mistake, as I believe the q8RHS bit regarding Earth's Euler function had its signs flipped.
elseif (i < 11) then
F(i) = -G * mSun * (sol(i-6) - sol(i-8))/distEtoS + mMoon * G *(sol(i-4) - sol(i-6))/distEtoM
Since the gravitational pull from the sun should be negative and from the moon positive given the way I've sketched it out. Here is the newest image
UPDATE 3
I have been made aware that my initial orbital velocity for the Moon was wrong -- it must be the sum of its orbital velocity around the moon plus the Earth's orbital velocity around the sun. My motions are now:
This was obviously much more reassuring to see, but I'm not sure if the Earth and Moon are behaving properly with regards to eachother. Zooming in, the moon does seem to oscillate to the left and right of the Sun's trajectory, so if the z axis was viewable this might make more sense, but it also might not.
The behavior above of the Moon's path moving to the left and right of the Earth's repeats constantly, but I'm not sure if this is still necessarily physically sensible.