Poor performance on the nqueens min-conflic search

Question

I am implementing the nqueens min-conflict search as mentioned by

Norvig, S., & Peter, J. R. and. (2014). Artificial Intelligence A Modern Approach. In Pearson (Vol. 58, Issue 12).

The authors mention this heuristic alone is super efficient:

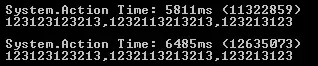
Yet when I implement it I cannot solve an over 5000 in less than a min. While the authors speed of million-queens in 50 iterations, my implementation often goes over the 1000 iterations for 5000-queens. Another question mentions similar result.

Any ideas on what I am doing wrong? Is it algorithmic or am I using a loop where I shouldn't?

update() is the main method by the way.





    list<unsigned> rowsInConflict(const unsigned currentState[]) {
        list<unsigned> rowsInConflict; //TODO change to map

        for (unsigned row = 0; row < boardSize; row++) {
            for (unsigned otherRow = 0; otherRow < boardSize; otherRow++) {
                if (isConflict(row, currentState[row], otherRow, currentState[otherRow])) {
                    rowsInConflict.push_front(row);
                    debug("row in conflict " + to_string(row));
                    rowsInConflict.push_front(otherRow);
                    //return rowsInConflict;
                }
            }
        }

        return rowsInConflict;
    }

    bool update(unsigned currentState[]) {
                unsigned randomRow, column;

        list<unsigned> conflictRows = rowsInConflict(currentState);
        if (conflictRows.empty()) {
            return true;
        }

        list<unsigned>::iterator it = conflictRows.begin();
        std::advance(it, rand() % conflictRows.size());
        randomRow = (unsigned) *it;

        column = getMinConflictColumn(currentState, randomRow);
        placeQueen(currentState, randomRow, column);


        return false;

    }



    void solve_nqueen(unsigned size, bool isVerbose) {

        unsigned rowSpace[size];






        while (!update(rowSpace)) {

            if (iterations >= 1000) {
                cout << "Random restart." << endl;
                intialize(rowSpace);
                iterations = 0;
            }
            iterations++;
        }
        printBoard(rowSpace);




    }

};

You're doing plenty of memory allocations with `rowsInConflict`, and I think you need a much more efficient method for choosing a random conflict. Also, the linked list is the most overrated data structure. — molbdnilo, Apr 20 '20 at 08:03
I usually just return the first conflict without populating the list. Still the result is the same. — Just_Alex, Apr 20 '20 at 08:25
`rand()` numbers distribution is quite poor in C++ even when using `srand`, instead you can try using `mt19937` for random numbers generating, also as others have mentioned do try to remove that list, it`s such a memory hog and memory operations are slow — Photon, Apr 20 '20 at 08:57
I understand that the number of iterations greatly depends of the initial position. You could for example initialise such that no queen is at the same column or at the same row. — Damien, Apr 20 '20 at 12:08
I should note that the results on my answer to the linked question were from a really quick-and-dirty implementation. I went on to write a slightly better version that solved 5000 queens in a little over 1.5 seconds starting from a "good" initial configuration. As @Damien said, the initial positions of the queens is crucial. I'll run a comparison when I get a chance, but the best configuration was given by placing a queen to each column in the row that caused the least conflicts with the previously-placed queens. — beaker, Apr 20 '20 at 15:06

beaker · Answer 1 · 2020-04-21T02:33:39.477

As I said in the comments, if you're trying to minimize the number of swaps, it's crucial to start with a good initial configuration. In my nQueens implementation, I have 3 different methods for generating the initial row for each queen:

For each queen, select a random row
Create a permutation of the numbers in 1..n corresponding to each queen's row number
Place each queen on the row with the least conflicts, breaking ties randomly

All of these approaches restrict each queen to a single column. The third method reuses the function I use find a new destination row when performing swaps.

Here are some sample runs on 5000 queens for each of the initial configurations:

# Board initialized by random rows
Number of queens = 5000, 100 reps
Average time per board: 1.57167
Average number of swaps: 3160.87

# Board initialized by shuffle
Number of queens = 5000, 100 reps
Average time per board: 1.17037
Average number of swaps: 2445.96

# Board initialized by min-conflict
Number of queens = 5000, 100 reps
Average time per board: 1.23296
Average number of swaps: 49.97

As you can see, method 3 gives us our target number of swaps, while the others require a lot more. In fact, the number of swaps required for this method is consistent from about 1000 queens on up.

Interestingly, the total time taken by each method does not vary nearly as much as the number of swaps. (All times include both setting up the initial board and moving the queens.)

Poor performance on the nqueens min-conflic search

1 Answers1