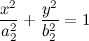1

Consider for the sake of simplicity the following equation (Burgers equation):

Burgers equation

Let's solve it using scipy (in my case scipy.integrate.ode.set_integrator("zvode", ..).integrate(T)) with a variable time-step solver.

The issue is the following: if we use the naïve implementation in Fourier space

enter image description here

then the viscosity term nu * d2x(u[t]) can cause an overshoot if the time step is too big. This can lead to a fair amount of noise in the solutions, or even to (fake) diverging solutions (even with stiff solvers, on slightly more complex version of this equation).

One way to regularize this is to evaluate the viscosity term at step t+dt, and the update step becomes

enter image description here

This solution works well when programmed explicitly. How can I use scipy's variable-step ode solver to implement it ? To my surprise I haven't found any documentation on this fairly elementary thorny issue...

Hippalectryon
  • 147
  • 6

1 Answers1

2

You actually can't, or on the other extreme, odeint or ode->zvode already does that to any given problem.

To the first, you would need to give the two parts of the equation separately. Obviously, that is not part of the solver interface. Look at DDE and SDE solvers where such a partition of the equation is actually required.

To the second, odeint and ode->zvode use implicit multi-step methods, which means that the values of u(t+dt) and the right side there enter the computation and the underlying local approximation.

You could still try to hack your original approach into the solver by providing a Jacobian function that only contains the second derivative term, but quite probably you will not achieve an improvement.

You could operator-partition the ODE and solve the linear part separately introducing 

vhat(k,t) = exp(nu*k^2*t)*uhat(k,t)

so that

d/dt vhat(k,t) = -i*k*exp(nu*k^2*t)*conv(uhat(.,t),uhat(.,t))(k)
Lutz Lehmann
  • 25,219
  • 2
  • 22
  • 51
  • I'm not sure i understand why it wouldn't fit in scipy's way of integrating ODEs. All I need is, in addition of the current *time*, the current *timestep* (since my gradient depends on (y, t, dt)), which scipy must know - but I don't know how to retrieve it – Hippalectryon Jul 02 '20 at 10:03
  • 1
    Any approach where the ODE function needs to access dynamical interna of the solver is, even if not wrong, then rather misguided. While the Euler method is the link from the analytical theory to numerical methods, it is not very representative of the behavior of higher-order methods. It is non-trivial to transfer a manipulation on the level of first order methods to a higher order. You have the best chances if you can represent it as a transformation of the ODE and then applying an Euler method to the transformed ODE. Then hope that applying the higher order method has the same effects. – Lutz Lehmann Jul 02 '20 at 10:20
  • Alright, thanks. As for the last part of your answer: wouldn't using vhat be more problematic computing-wise ? Since the term exp(nu k^2 t) in the derivative would lead to a much greater humerical blowup that nu*k^2*u – Hippalectryon Jul 03 '20 at 09:28
  • But the convolution contains twice the inverse factor, so that this balances out somewhat. Then again, balancing out numerical overflow and underflow is not really a stable operation. However, this takes out the problematic linear term and contains its contribution exactly, so in theory should make the equation less stiff and allow larger time steps. – Lutz Lehmann Jul 03 '20 at 10:16