I was reading the book titled "The Way of Z: Practical Programming with Formal Methods by Jonathan Jacky" and in chapter 18 (8 Queen problem), the author provided a Z notation based formal solution to the famous 8 queen problem. He tried to solve the diagonal part by connecting it to a straight line equation. The variables used in the solutions are:
Then the straight-line equations to solve the diagonal part are:
 where file represents a row here and rank represents a column.
The Image that is provided to help us understand the diagonals is:
where file represents a row here and rank represents a column.
The Image that is provided to help us understand the diagonals is:
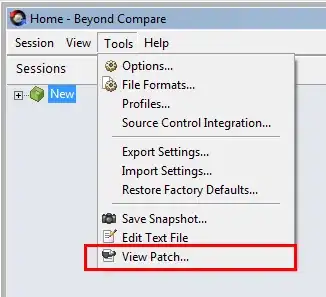
The solution works as follows: The file(row) number 1 is highlighted in blue. The rank(column) 1 is highlighted in red. The solution goes from downside to up and from left to right.
I want to calculate the up and down function values for the square at file(row)=4 and rank(column)=6 (highlighted in yellow).
So,
up = rank - file = 6 - 4 = 2
down = rank + file = 6 + 4 = 10
as can be seen in the image above, the up diagonal line does cut the left edge for y-intercept at point 2. But the down diagonal line cuts the y-intercept at point 9 (instead of 10). There is a difference of 1. And this difference is for all square. I want to know what piece am I missing in this case? Why is there always a difference in the case of the down arrow (and not in the case of the up arrow)?
I am also attaching the full Z notation based solution for reference here: