Most simply:
Map2 = # @@@ Partition[#2, 2, 1] &;
Or, possibly using less memory, but running a bit slower:
Map2[f_, lst_] := Developer`PartitionMap[f @@ # &, lst, 2, 1]
Also, be aware of Differences and Accumulate, which are related.
Other ways:
Inner[#, Most@#2, Rest@#2, List] &
Notice that in this one List could be a different function.
MapThread[#, {Most@#2, Rest@#2}] &
Most@MapThread[#, {#2, RotateLeft@#2}] &
Rest@MapThread[#, {RotateRight@#2, #2}] &
Table[# @@ #2[[i ;; i + 1]], {i, Length@#2 - 1}] &
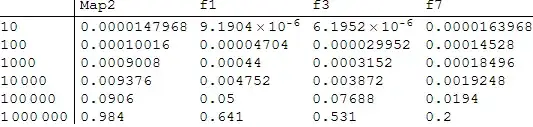
Now, the timings. I will make use of Timo's timeAvg.
f1 = # @@@ Partition[#2, 2, 1] &;
f2[f_, lst_] := Developer`PartitionMap[f @@ # &, lst, 2, 1]
f3 = Inner[#, Most@#2, Rest@#2, List] &;
f4 = MapThread[#, {Most@#2, Rest@#2}] &;
f5 = Most@MapThread[#, {#2, RotateLeft@#2}] &;
f6 = Table[# @@ #2[[i ;; i + 1]], {i, Length@#2 - 1}] &;
timings =
Table[
list = RandomReal[99, 10^i];
func = Plus;
timeAvg[#[func, list]] & /@ {f1, f2, f3, f4, f5, f6},
{i, 6}
];
TableForm[timings,
TableHeadings -> {10^Range@6, {"f1", "f2", "f3", "f4", "f5", "f6"}}]
ListLogPlot[timings\[Transpose], Joined -> True]

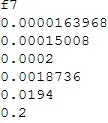
The numbers on the left side of the table are the length of the list of real numbers for each run.
Note that the graph is logarithmic.
Here are the bytes of memory used while processing the longest list (1,000,000):
After doing the timings above, I found I can make f6 faster by eliminating Apply (@@). It is now clearly the fastest on longer lists. I will not add it to the table above because that is already wide enough, but here is the function and its timings:
f7 = Table[#2[[i]] ~#~ #2[[i + 1]], {i, Length@#2 - 1}] &;