0

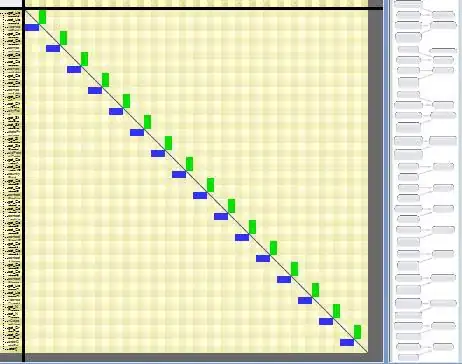
I have some data on regular structured grid and I need to estimate the normal to the geometry surface and the area at the nodes intersecting with the geometry.

enter image description here

as you can see in the image I want the surface area and normals of the geometry in this case the triangle in the image (interior points have values of zero and exteriors 1). I estimated the normals as the gradients as

equation

where "C" is 1 outside the geometry and 0 inside it (see the top image).

I cannot figure out how to calculate surface area though. The reason is I want to then use the approach to do surface integrals like:

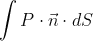
force

where P for example would be a field value which would be 0 inside the geomoetry as in the below image

enter image description here

Any comment is really appreciated.

EDIT

I managed to significantly improve the outer edge detection and normal calculations. Basically, I used a Gaussian filter to first smooth the color field. I then defined a band threshold to detect cells within the threshold as the edge cells. This combined with gradient estimation as before, resulted in very good surface normal estimations.

Ashkan Rafiee
  • 33
  • 9
  • It is not clear for me what do you want exactly. What is your geometry? What is C? where is the grid? – s.ouchene May 09 '20 at 07:54
  • area is `count of points * size of point` ... for normals just find the vertexes what you seems to already done on your second image just compute the location of max/min in the gradients and then just use convex hull and rotation of each line by 90 deg ... – Spektre May 09 '20 at 08:03
  • @Navaro the geometry is triangle in these images. The C is a scalar with values of 0 inside the triangle and 1 outside of it. I did not show the mesh but mesh is simply a regular grid here. so at each point of the grid we have C values which is the first image. – Ashkan Rafiee May 09 '20 at 08:41
  • @Spektre the second image is not the max and min of vertices. It is basically the pressure field which I want to integrate over the geometry surface. I basically want the mathematical approach which I can use for more complex geometries and also 3D cases. – Ashkan Rafiee May 09 '20 at 08:45
  • I am assuming simply ds=sqrt(dx^2 +dy^2) at any point. – Ashkan Rafiee May 09 '20 at 08:58
  • @AshkanRafiee then you can use DIP detector similar to this [OpenCV Birdseye view without loss of data](https://stackoverflow.com/a/39316776/2521214) to obtain the shape vertex points, or detect outline, lines by Hough transform or by morphologic operators, or by count of empty space neighbors , or detect angle of slope of edge (of length bigger then just 2 pixels usually 15 is enough) and join similar edges, or use convex hull on the point cloud ... there are many options to choose from these are just a few I can think of right now – Spektre May 10 '20 at 07:27

0 Answers0