I am creating my own 2D paint engine that is able to stroke and fill paths. I am having trouble with the corners of line segments connecting.
The way I do it is calculate the normal of each line segment and in the corners, I use the average normal of the two adjacent edges. To calculate the vertices for the thickness of the line, I use the line segment coordinate and subtract/add the average normal multiplied by half the line thickness.
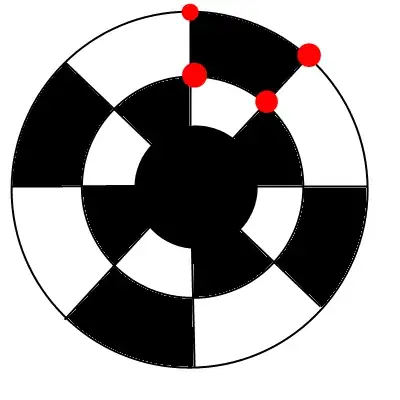
On the sketch, this means that I calculate the light blue normals (I use them for the free line endings too, except when it's a loop) and calculate the average of the two for the corner, which is the red normal (and the green is the negative version).
I scale the normals with a 1/2 thickness (orange shape) to get the vertices.
Although the direction of the red/green normals are ok, the magnitude calculation isn't correct for the corners.
This looks quite nice, but not good enough: depending on the angle of the corner, the line gets thinner/thicker than the requested thickness.
So taking the average normal doesn't seem to be enough.
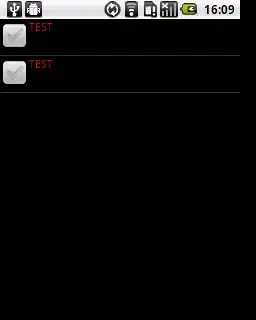
This is how it looks: look at how bad the corners look... can anyone give me tips on how to improve this?
p.s. no need to tell me to use a 3rd party library and forget about this problem