How to use the replicate function in R to repeat the function

Question

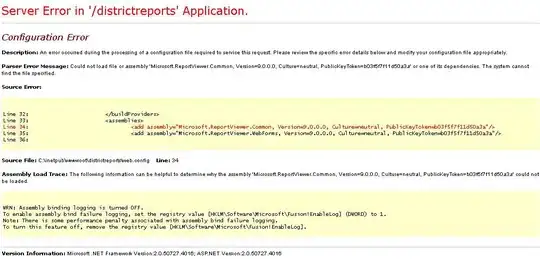
I have a problem when using replicate to repeat the function.

I tried to use the bootstrap to fit a quadratic model using concentration as the predictor and Total_lignin as the response and going to report an estimate of the maximum with a corresponding standard error.

My idea is to create a function called bootFun that essentially did everything within one iteration of a for loop. bootFun took in only the data set the predictor, and the response to use (both variable names in quotes).

However, the SD is 0, not correct. I do not know where is the wrong place. Could you please help me with it?

# Load the libraries
library(dplyr)
library(tidyverse)

# Read the .csv and only use M.giganteus and S.ravennae.
dat <- read_csv('concentration.csv') %>% 
  filter(variety == 'M.giganteus' | variety == 'S.ravennae') %>% 
  arrange(variety)
# Check the data
head(dat)

# sample size
n <- nrow(dat)

# A function to do one iteration
bootFun <- function(dat, pred, resp){
  # Draw the sample size from the dataset
  sample <- sample_n(dat, n, replace = TRUE)

  # A quadratic model fit
  formula <- paste0('resp', '~', 'pred', '+', 'I(pred^2)')
  fit <- lm(formula, data = sample)

  # Derive the max of the value of concentration
  max <- -fit$coefficients[2]/(2*fit$coefficients[3])

  return(max)
}

max <- bootFun(dat = dat, pred = 'concentration', resp = 'Total_lignin' )

# Iterated times
N <- 5000

# Use 'replicate' function to do a loop
maxs <- replicate(N, max)

# An estimate of the max of predictor and corresponding SE
mean(maxs)
sd(maxs)

Welcome! Please provide `dput(dat)`, needless to say that we cannot access your .csv file. Read here how we ask reproducible questions: https://stackoverflow.com/questions/5963269/how-to-make-a-great-r-reproducible-example/5963610#5963610 — jay.sf, Jun 18 '20 at 03:47
You're replicating the *result* of a *single* function call N times, not replicating the function call N times. — Ritchie Sacramento, Jun 18 '20 at 03:58
See this [SO post](https://stackoverflow.com/a/47578665/8245406). — Rui Barradas, Jun 18 '20 at 04:57

Rui Barradas · Accepted Answer · 2020-06-18T05:07:29.370

Base package boot, function boot, can ease the job of calling the bootstrap function repeatedly. The first argument must be the data set, the second argument is an indices argument, that the user does not set and other arguments can also be passed toit. In this case those other arguments are the predictor and the response names.

library(boot)

bootFun <- function(dat, indices, pred, resp){
  # Draw the sample size from the dataset
  dat.sample <- dat[indices, ]

  # A quadratic model fit
  formula <- paste0(resp, '~', pred, '+', 'I(', pred, '^2)')
  formula <- as.formula(formula)
  fit <- lm(formula, data = dat.sample)

  # Derive the max of the value of concentration
  max <- -fit$coefficients[2]/(2*fit$coefficients[3])

  return(max)
}

N <- 5000
set.seed(1234)  # Make the bootstrap results reproducible

results <- boot(dat, bootFun, R = N, pred = 'concentration', resp = 'Total_lignin')

results
#
#ORDINARY NONPARAMETRIC BOOTSTRAP
#
#
#Call:
#boot(data = dat, statistic = bootFun, R = N, pred = "concentration", 
#    resp = "Total_lignin")
#
#
#Bootstrap Statistics :
#      original        bias    std. error
#t1* -0.4629808 -0.0004433889  0.03014259
#


results$t0  # this is the statistic, not bootstrapped
#concentration 
#   -0.4629808

mean(results$t)  # bootstrap value
#[1] -0.4633233

Note that to fit a polynomial, function poly is much simpler than to explicitly write down the polynomial terms one by one.

formula <- paste0(resp, '~ poly(', pred, ',2, raw = TRUE)')

Check the distribution of the bootstrapped statistic.

op <- par(mfrow = c(1, 2))
hist(results$t)
qqnorm(results$t)
qqline(results$t)
par(op)

Test data

set.seed(2020)  # Make the results reproducible
x <- cumsum(rnorm(100))
y <- x + x^2 + rnorm(100)
dat <- data.frame(concentration = x, Total_lignin = y)

How to use the replicate function in R to repeat the function

1 Answers1