4

"x","y" are two long long type variables in c++ to which i have assigned two different numbers.

Variable type is long long but i have assigned decimals to the integer.

so i expected that it will trim the decimal part and display only integer part.

it trimmed off the numbers after the decimal and retured an integer.

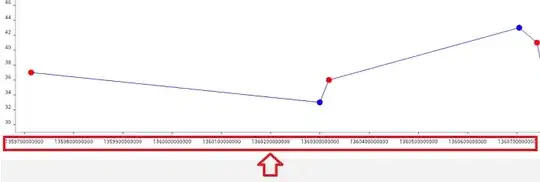
enter image description here

Output :

enter image description here

i was expecting floor() of x but it returned some integer ending with 6 instead of 5, i mean it returned ceil(x).but in the second case it returned floor(y).

and its only occurring when the integer is too long.

So what might be the possible reason for this ?

I am using minGW c++17 version on visual studio code .. but same is happening with online compiler also.

Bill Lynch
  • 80,138
  • 16
  • 128
  • 173
Cheemakurthi Mukesh
  • 671
  • 2
  • 6
  • 9
  • 4
    See [Is floating point math broken?](https://stackoverflow.com/questions/588004/is-floating-point-math-broken). – 1201ProgramAlarm Jul 01 '20 at 19:09
  • 1
    I'd suggest [examining the actual value you get](https://i.imgur.com/Kw2ezSB.png) without integers in the picture. – chris Jul 01 '20 at 19:15

1 Answers1

13

Each initialization involves two conversions, first from the decimal numeral in the source text to double, and then from double to long long.

Let’s discuss the second declaration first. Because 2.001 is a double constant, the decimal source text 2.001 must be converted to double. Assuming your C implementation uses IEEE-754 binary64, the result is 2.000999999999999889865875957184471189975738525390625. Then, for the initialization, this double value is converted to long long. This conversion to an integer type discards the fraction, so the result is 2.

In the first declaration, when 9223372036854775.001 is converted to double, the result is 9223372036854776. This is because the two double numbers nearest 9223372036854775.001 are 9223372036854774 and 9223372036854776. The latter one is closer, so it is chosen. Then this double value is converted to long long. There is no fraction part, so the result is simply 9223372036854776.

Thus, the first conversion rounds up because it is not simply converting to the nearest long long value. It first has to round to the nearest double value. And, at the scale of that number, the double format does not have enough resolution to represent every integer. It is representing only every second integer: 9223372036854770, …772, …774, …776, …778, and so on. So 9223372036854775 is not a candidate.

Eric Postpischil
  • 195,579
  • 13
  • 168
  • 312
  • 3
    @Hack06: A 64-bit floating-point format can represent at most 2^64 numbers (fewer actually, because some bit patterns are reserved for special meanings). There are infinitely many integers. Therefore, 64 bits is incapable of representing every integer. – Eric Postpischil Jul 01 '20 at 19:21
  • then let them represent whatever they can in a sequential order, not just wtf they want... – Hack06 Jul 01 '20 at 19:23
  • 2
    @Hack06: More specifically, a floating-point format consists of a sign, a number of a fixed width in some base (often 2), and an exponent, and the value represent is the number multiplied by the base raised to the power of the exponent. When the exponent is sufficiently large, its multiplication of the fixed-width number means the low digits of that number are scaled beyond the value of 1, so they cannot be incremented by single-integer increments. – Eric Postpischil Jul 01 '20 at 19:24
  • 1
    @Hack06: An example of a floating-point format is a sign, three decimal digits, and an exponent. When the exponent is −4 (note: where the starting point of the exponent is is arbitrary ), this format represents numbers from .0100 to .0999. When it is −3, it represents numbers from .100 to .999. When it is −2, it represents numbers from 1.00 to 9.99. When it is −1, it represents numbers from 10.0 to 99.9. When it is 0, it represents numbers from 100 to 999. When it is 1, it represents numbers from 1000 to 9990. At that point, it cannot represent every integer, because the scale is too big. – Eric Postpischil Jul 01 '20 at 19:26
  • 1
    @Hack06: A `float` and a `double` uses scientific notation. It's stored as 1.0240000486373901 * 2^53. The first part can only have 23 bits, so it can't hold every integer precisely in sequential order. The type that _does_ do that is... `long long`. You can also do what you want with fixed point types, but they hold _much_ smaller ranges than a float type as a result. – Mooing Duck Jul 01 '20 at 19:28
  • 3
    @Hack06: Highly recommended: https://www.itu.dk/~sestoft/bachelor/IEEE754_article.pdf It's a classic. – Howard Hinnant Jul 01 '20 at 19:30
  • Thanks for enlightenment! I don't know why I missed this part for so long... I knew that there's always a rounding issue with floating point numbers and for precision we need to operate on integer numbers, but not how floating point numbers are represented in the computer memory actually. – Hack06 Jul 01 '20 at 19:31
  • @Hack06: Working with integers gives you different precision, not always better. Floating-point has better precision with small numbers and worse with large numbers. For example, for 8/5, integer arithmetic gives an answer of 1 instead of 1⅗, which is an error of 37.5%. The IEEE-754 32-bit binary format gives an answer of 1.60000002384185791015625, which has an error of only 0.00000149%, so floating-point is hugely more precise than integer in this case. And, of course, with the slightest overflow, integer arithmetic goes completely haywire, whereas floating-point degrades gracefully. – Eric Postpischil Jul 01 '20 at 19:36
  • By precision I meant exact values, not the granularity. For example while counting money in cents, one should use integers to represent the amounts, instead of floating point values. But thanks for the hint. – Hack06 Jul 01 '20 at 19:41
  • u have mentioned nearest numbers are ...........................74 and ...........................76 , why didnt u mentioned .....................75. – Cheemakurthi Mukesh Jul 17 '20 at 03:26
  • @CheemakurthiMukesh: 9223372036854775 is not representable in a `double`. A `double` represents numbers as a 53-bit integer (or fixed-point number; these are equivalent aside from the scaling used) multiplied by a power of two. The largest 53-bit integer is 9007199254740991, so numbers around 9223372036854775 must be represented as a 53-bit integer multiplied by two (two to the first power). So they are all even. 9223372036854774 is represented as 4611686018427387•2, and 9223372036854776 is represented as 4611686018427388•2. There is no way to represent 9223372036854775. – Eric Postpischil Jul 17 '20 at 11:17