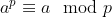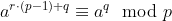CSES exponentiation 2 problem in handling mod=1000000007(10^9+7)

Question

#include <bits/stdc++.h>
using namespace std;
using ull = unsigned long long;
#define tt ull tt; cin>>tt; while(tt--)

ull calExpo(ull x, ull y, ull mod){
    ull res=1;
    while(y>0){
        if(y&1){
            res=(res*x)%mod;
        }
        y=y>>1;
        x=(x*x)%mod;
    }
    return res;
}

void solve(void){
    tt{
        ull x,y,z;
        cin>>x>>y>>z;
        ull mod=1000000007;
        ull t= calExpo(y,z,mod-1); // doubt is in this line
        cout<<calExpo(x,t,mod)<<endl;
    }
}

int main(void){
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    
    // #ifndef ONLINE_JUDGE
    //  freopen("input.txt", "r", stdin);
    //  freopen("output.txt", "w", stdout);
    // #endif

    solve();
    return 0;
}

i wrote code for CSES problem https://cses.fi/problemset/task/1712/ (problem description in short: give n test cases for each n there are 3 integer values a,b,c we have to calculate a^b^c (a to the power b and b to the power c) given mod=10^9+7 ) i was getting error when i passed only (mod) as third argument while calling function (calExpo) for first time (in line ull t= calExpo(y,z,mod-1); ) then i passed mod-1 and it passed all test cases . please tell me what is the reason behind that?

`#define tt ll tt; cin>>tt; while(tt--)` probably gets you an instant downvote. — drescherjm, Jul 16 '20 at 14:43
Does not compile. Non-standard include. Does not define `ll`. Could be running into problems because of ill-advised `using namespace std;`. Doesn't mention the input to use. Doesn't mention the expected output from the input to use. Doesn't mention the actual output from the input to use. — Eljay, Jul 16 '20 at 14:54
Duplicate? Concerning modular exponentiation, you will find useful information here: https://stackoverflow.com/questions/11448658/modular-exponentiation. If P is prime, `phi(P)=P-1` ! — Damien, Jul 16 '20 at 14:58
Sorry I just removed my template, that ll t; remained unnoticed ..sorry for that — , Jul 16 '20 at 17:23

score 1 · Answer 1 · answered Jul 16 '20 at 15:36

1

The reason why taking mod-1 is correct is because of Fermat's little theorem:

$a^p \equiv a \mod p$

Therefore:

$a^{r\cdot(p-1) + q} \equiv a^q \mod p$

In your case you are representing b^c as r * (p-1) + q which is essentially taking it modulo p-1.

answered Jul 16 '20 at 15:36

Jacob Dlougach

308
1
6

Something is really weird with that font for the equations on chrome on windows. Edit: I see it does not work in the StackOverflow dark theme. – drescherjm Jul 16 '20 at 16:33

CSES exponentiation 2 problem in handling mod=1000000007(10^9+7)

1 Answers1