difference of complexity in ordering and sorting?

Question

I'm trying to understand the complexity of numpy array indexing here.

Given a 1-d numpy array A. and b = numpy.argsort(A)

what's the difference in time compleixty between np.sort(A) vs A[b] ?

for np.sort(A), it would be O(n log (n)), while A[b] should be O(n) ?

score 0 · Answer 1 · answered Jul 30 '20 at 17:30

0

Under the hood argsort does a sort, which again gives complexity O(n log(n)). You can actually specify the algorithm as described here

To conclude, while only A[b] is linear you cannot use this to beat the general complexity of sorting, as you yet have to determine b (by sorting).

answered Jul 30 '20 at 17:30

Matthias Sokolowski

83
5

yeah, I'm aware of that, but I'm more interested in the complexity of `A[b]`, as stated in the question, `b` was given. – yupbank Jul 30 '20 at 17:32
If space complexity is irrelevant, you can fill `C[i] = A[b[i]]` in linear time. If space is constant, elements of A have to be swapped in some fancy way, which might not be trivial. – Matthias Sokolowski Jul 30 '20 at 17:43

score 0 · Answer 2 · answered Jul 30 '20 at 17:42

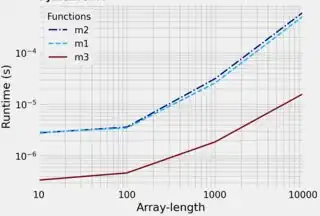
Do a simple timing:

In [233]: x = np.random.random(100000)                                                               
In [234]: timeit np.sort(x)                                                                          
6.79 ms ± 21 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
In [235]: timeit x[np.argsort(x)]                                                                    
8.42 ms ± 220 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
In [236]: %%timeit b = np.argsort(x) 
     ...: x[b] 
     ...:                                                                                           
235 µs ± 694 ns per loop (mean ± std. dev. of 7 runs, 1000 loops each)
In [237]: timeit np.argsort(x)                                                                         
8.08 ms ± 15.3 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

Timing only one size doesn't give O complexity, but it reveals the relative significance of the different steps.

If you don't need the argsort, then sort directly. If you already have b use it rather than sorting again.

thanks! yeah i did the same thing, but still i need somehow use the big o notation for `A[b]` in some technical document, where i'm not exactly sure `O(n)` is correct or not. — yupbank, Jul 30 '20 at 17:44
A quick test with smaller `x` shows the `A[b]` is roughly `O(n)`. It has to copy `b.shape` items from `A` to a new new array, Details of that are buried in complex `c` code - determining the size of `b`, allocating the target space, using `c` pointer indexing to copy from one data buffer to the other. — hpaulj, Jul 30 '20 at 17:51
In the real world, operations are a mix of times. There's a setup time, operation time etc. So it might be `a*O(1) + b*O(n) + ...` For small arrays the setup time can dominate, for large ones the O(n) etc. Also with very large arrays, memory management becomes an issue. — hpaulj, Jul 30 '20 at 17:57

score 0 · Answer 3 · answered Jul 30 '20 at 21:03

Here is a visual comparison to see it better:

#sort
def m1(A,b):
  return np.sort(A)

#compute argsort and them index
def m2(A,b):
  return A[np.argsort(A)]

#index with precomputed argsort
def m3(A,b):
  return A[b]

A = [np.random.rand(n) for n in [10,100,1000,10000]]

Runtime on a log-log scale:

difference of complexity in ordering and sorting?

3 Answers3