1

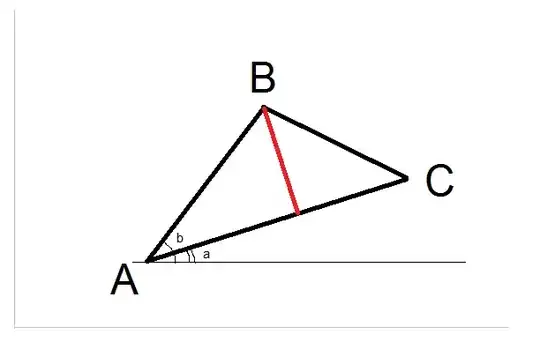
For a polygon which is defined as a hole in a triangular mesh, with each vertex defined with [x, y, z] coordinates, how can the inner angle between each edge be calculated? The hole is not planar, but can have arbitrary curvature.

The smallest angle between the edges can be calculated with the dot product. However, I want the inner angle in the interval [0, 360] degrees, and therefore need to know whether the inner angle is convex or concave. If it is concave, I can simply add 180 degrees to the angle acquired from the dot product.

Perhaps there is a way to use the normals of the surrounding triangles somehow?

enter image description here

codetiger
  • 2,650
  • 20
  • 37
deeplearningrobot
  • 13
  • 3
  • In what programming language do you want/have to solve this problem? This will have also consequences for your data structures. – jmizv Aug 12 '20 at 09:38
  • There is fairly complex hole filling algorithms already available. I don't think it is as easy as you have explained. Finding hole in mesh itself is a challenging task. – codetiger Aug 12 '20 at 11:55
  • C++. Current choice of data structure is a std::vector, which contains the vertices which define the hole. I've seen that e.g. Liepa's hole filling algorithm uses the minimum dihedral angle as a cost function, while the approach I'm trying to implement is a variant of the advancing front method which I think uses the minimum vertex angle instead. – deeplearningrobot Aug 12 '20 at 12:23
  • However, I think this problem is strictly mathematical. For instance, if the hole was planar, whether an angle is convex/concave could be determined by finding the normal of the hole and comparing it with the cross product of the two edges defining the angle (by the sign of their dot product). Unfortunately, this won't work when the hole is curved. – deeplearningrobot Aug 12 '20 at 12:32

1 Answers1

0

If you can consistently define the order of vertices along the boundary, you can determine whether an edge is convex or concave by drawing a line segment to the angle edges and comparing the central vertex to that line segment:

enter image description here

As seen in the figure, I've defined a segment connecting the edges of an angle defined by vertices 1, 2, and 3. So long as your vertex ordering is consistent, the angle is either convex or concave based on whether the middle point of the angle (vertex 2 here) is to the left or the right of the line segment.

A.Comer
  • 810
  • 7
  • 17
  • Yes, the vertices are ordered clounter-clockwise (if looked at such that all the surrounding triangles' normals are pointing outwards). The page you linked to for determining whether the middle point is to the left or the right of the line segment seems to be for the 2D case. How can this be done in 3D? In particular, I don't see how to interpret the result for edges connected to triangles with normals in the negative z direction. – deeplearningrobot Aug 12 '20 at 14:38
  • The 3 vertices which define the angle also define a plane, so this actually *is* a 2D case. You would project your points onto the plane defined by your 3 vertices and then do the 2D left/right check – A.Comer Aug 12 '20 at 15:37
  • Sorry, but I still don't see exactly how to apply this method. If I do a projection to the XY plane by simply removing the z component, the three vertices could be ordered in both a clockwise or counter-clockwise manner (due to the conditions stated in my previous comment). As far as I see, the left/right check will then break for one of the vertex orders. What's the trick to avoid this pitfall? – deeplearningrobot Aug 14 '20 at 15:49
  • You don't project onto the XY plane, you project onto the plane defined by the edge vertices (vertices 1, 2, and 3 in the figure) – A.Comer Aug 14 '20 at 17:37