Just trying to understand the linear probing logic.
With as hashtable using open addressing, how can you ever confirm that an element isn't in the table.
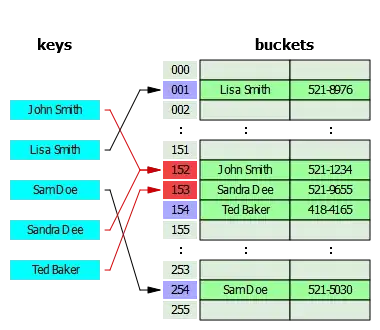
For example, say you had a 10 bucket hashmap. Suppose you hash a key, and insert it. Now, if element A and B are to be inserted and hash and reduce to the same bucket then element A and B if using a linear probe will likely be next to each other.
Now, just because a bucket is empty, does not seem to mean that an element doesn't exist in the map. e.g. You search for element B after element A is first removed. First you get an empty bucket where you expect B to be, but you need to probe one more and you'll find B. It's really is there. If that logic is correct then won't you have to search the entire table to confirm whether a key is not there? i.e. O(n) performance everytime.
What I'm saying is, don't you need to go through the whole map to truly confirm it's not there?
With a separate chaining approach to hashmap's that problem doesn't exist.
If John Smith is deleted, and we try to locate Sandra Dee.
Or with linear addressing are you meant to move elements around so that there are no holes as such. i.e. If John Smith is deleted should elements from 152 to 154 be shifted back one place? It don't really see that in the description but that might make some sense. Except if ted baker hashed to 154 and not 153 as described. Requires a bit more work than I thought.
Might just go with a simple linked list at each bucket.