This becomes a completely mathematical problem. You need to find all non-negative solution triplets for linear diophantine equation 3a+7b+10c=60.
The main idea of finding solutions for this equation can be illustrated using generating functions (polynomials). Let us take three such polynomials:
A=1+x^3+x^6+x^9+...+x^60
B=1+x^7+x^14+x^21+...+x^56
C=1+x^10+x^20+x^30+...+x^60
If you multiply them, you see that each term x^n can be expressed as a product of x^a, x^b and x^c, every of these terms are taken from A, B and C respectively.
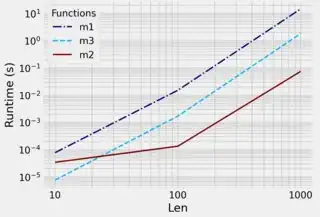
Brute-force approach. You need to define multiplication of these polynomials that keeps track of terms that were multiplied, just like this:
[0, 3, 6] * [0, 7, 14] * [0, 10] = [(0,0,0), (0,0,10), (0,7,0), (0,7,10), (3,0,0), (3,0,10), (3,7,0), (3,7,10), (6,0,0), (6,0,10), (6,7,0), (6,7,10)]
Lists don't have * operator in Python but, fortunately, you can use itertools.product method instead. This is a complete sulution:
from itertools import product
A, B, C = range(0, 61, 3), range(0, 61, 7), range(0, 61, 10)
triplets = list(product(A, B, C)) # all triplets
suitable_triplets = list(filter(lambda x: sum(x)==60, triplets)) #triplets that adds up to 60
print([[a//3, b//7, c//10] for a, b, c in suitable_triplets])
Vectorised brut-force. This is based on previous script, replacing all the loops with numpy actions:
import numpy as np
l = np.array([3,7,10])
s = 60
unknowns = [range(0, s+1, n) for n in l]
triplets = np.stack(np.meshgrid(*unknowns), axis=-1).reshape(-1, len(unknowns))
suitable_triplets = triplets[np.sum(triplets, axis=1) == s]
solutions = suitable_triplets//l
Mathematical approach. In general, solving linear diophantine equations is hard. Look through this SO answer. It says that sympy is able to find a parametrised solution only but it can't identify domain:
import sympy as sp
from sympy.solvers.diophantine.diophantine import diop_solve
x,y,z = sp.symbols('x y z')
solution = diop_solve(3*x + 7*y + 10*z-60)
And the output of solution is (t_0, t_0 + 10*t_1 + 180, -t_0 - 7*t_1 - 120).
Optimised solution is possible using Sage but you are required to download Linux Operating System in this case :D