1

This problem may be related to this post.

This problem also asked here but with a different taste.

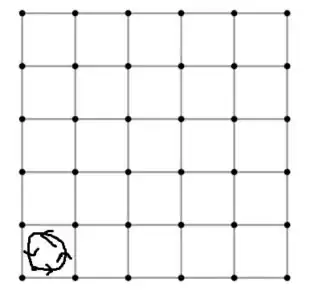
Consider an (undirected) square graph with a periodic boundary condition. Then find a complete cycle graph with length equal to 4. now I want to assign a unique representative to each cycle from its elements. Therefore in a square graph with n_v vertex i will find n_f=n_v 4-cycles and n_v representative for the cycles. For the square graph, everything is simple. just assign the bottom left vertex of each plaque(4-cycles).

enter image description here

(i just show first 4-cycle)

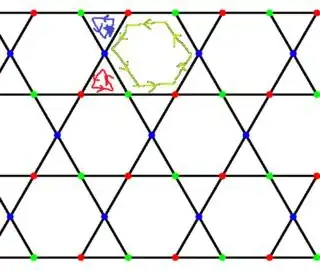
Now, I want to generalize it for other structures. consider (undirected) kagome graph with proper boundary condition,

enter image description here

(here I just show 3 distinct cycles)

In this case for assigning a vertex to cycles cover, you need three different length cycles. which show by similar color with the assigned vertex. However, now I want to generalize this to other complicated graphs. I want to know is this problem has a name and about its possibility or algorithm. For example, we cannot do it in a triangular graph:

enter image description here

Rasoul-Ghadimi
  • 111
  • 4
  • By cycle, do you mean face in the planar graph as you have embedded it? – David Eisenstat Aug 28 '20 at 12:52
  • @DavidEisenstat, yes. Actually I define cycle to identifies faces. – Rasoul-Ghadimi Aug 29 '20 at 04:00
  • I know a fair amount about planar graphs, but with the periodic boundary condition, we're moving into a part of the subject I know less about. It seems to me that you're dealing in graphs on a torus. A necessary condition is V = F (number of vertices equals faces), which implies that the average degree of both must be 4 by Euler's formula (which rules out the triangles). Interestingly both of your positive examples are self-dual, but I don't see why that should be a necessary or sufficient condition. – David Eisenstat Aug 30 '20 at 02:47
  • Oh, no the second isn't self dual. – David Eisenstat Aug 30 '20 at 02:55

1 Answers1

0

This problem solved here.

  • I)Let show all faces and vertices by \alpha_i, where i contain vertices and faces.
  • II) make a graph which relates \alpha_i (from i in face group) to \alpha_j (to j in vertex group), if j(vortex) belong to i(face).
  • III) find the independent edge set of this graph gives for any vortex a face.

Please see here for additional information.

Rasoul-Ghadimi
  • 111
  • 4