create interpolated polygons from GPS data with value column

Question

I have some GPS data with a value assigned to each point (think like air quality). I can plot those points, with folium for instance, and map the value to the size of a circle, like this:

import pandas, numpy, folium
lat = numpy.random.uniform(45, 45.01, 250)
lon = numpy.random.uniform(3, 3.02, 250)
value = numpy.random.uniform(0,50,250)
df = pandas.DataFrame({'lat': lat, 'lon': lon, 'value': value})
mymap = folium.Map(location = [lat.mean(), lon.mean()], tiles="OpenStreetMap", zoom_start=14)
for elt in list(zip(df.lat, df.lon, df.value)):
    folium.Circle(elt[:2], color="blue", radius=elt[2]).add_to(mymap)
mymap.save('mymap.html')

And I would like to treat this data, interpolate it and create a shapefile as the output, with interpolated polygons containing the average value and showing areas of high and low value (fake picture on the right). The limit of the polygons would auto-generated, of course, from the interpolation.

How can I achieve this? Because i have tried using HeatMap tool in folium, but it is designed to interpolate the density of points, not the value associated with each point! I hope it's not too complex..Thanks, note: I use folium but i'm ok with other python libraries.

Answer 1

We can feed the values to HeatMap in folium as weights (see the data parameter in documentation).

Here's an example. I've divided values in the bottom half of the box by 5 to demonstrate that despite the relatively uniform density of data points, the heat map clearly shows higher magnitudes in the upper half of the picture:

import pandas as pd
import numpy as np
import folium
from folium.plugins import HeatMap
import matplotlib as mpl

# parameters
n = 250                     # number of points
lat0 = 40.7                 # coordinates will be generated uniformly with
lon0 = -73.9                # lat0 - eps <= lat < lat0 + eps
eps = 0.1                   # lon0 - eps <= lon < lon0 + eps
v_min, v_max = 0, 100       # min, max values

# generating values
lat = np.random.uniform(lat0 - eps, lat0 + eps, n)
lon = np.random.uniform(lon0 - eps, lon0 + eps, n)
value = numpy.random.uniform(v_min, v_max, n)
df = pandas.DataFrame({'lat': lat, 'lon': lon, 'value': value})

# to demonstrate the effect of weights on the heatmap,
# we'll divide values below the center of the box by K = 5
K = 5
df.loc[df['lat'] < lat0, 'value'] /= K

# plotting the map, both the points themselves and the heatmap
m = folium.Map(location = [lat0, lon0], tiles="OpenStreetMap",
               zoom_start=11, width=400, height=400)
for elt in list(zip(df.lat, df.lon, df.value)):
    folium.Circle(elt[:2], color="white", radius=elt[2]).add_to(m)

# df.values used here is a (250, 3) numpy.ndarray
# with (lat, lon, weight) for each data point
HeatMap(data=df.values, min_opacity=0.1).add_to(m)

m

Output:

---

Update:

Here's a slightly different approach, not using the built-in HeatMaps (which is probably currently a better option in light of https://github.com/python-visualization/folium/issues/1271, as mentioned by @agenis).

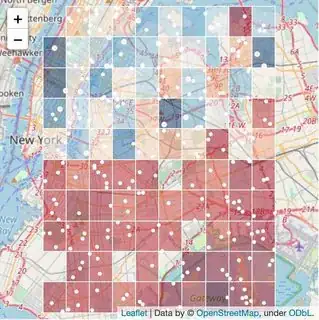
We first transform our data, making the grid of squares, where value for each square is the average of original data point values lying within that cell (so it does not depend on the number of points within that cell, only their values).

Then we can visualise those squares by plotting GeoJson polygons on the map. Here's an example:

# define the size of the square
step = 0.02

# calculate values for the grid
x = df.copy()
x['lat'] = np.floor(x['lat'] / step) * step
x['lon'] = np.floor(x['lon'] / step) * step
x = x.groupby(['lat', 'lon'])['value'].mean()
x /= x.max()
x = x.reset_index()

# geo_json returns a single square
def geo_json(lat, lon, value, step):
    cmap = mpl.cm.RdBu
    return {
      "type": "FeatureCollection",
      "features": [
        {
          "type": "Feature",
          "properties": {
            'color': 'white',
            'weight': 1,
            'fillColor': mpl.colors.to_hex(cmap(value)),
            'fillOpacity': 0.5,
          },
          "geometry": {
            "type": "Polygon",
            "coordinates": [[
                [lon, lat],
                [lon, lat + step],
                [lon + step, lat + step],
                [lon + step, lat],
                [lon, lat],
              ]]}}]}


# generating a map...
m = folium.Map(location=[lat0, lon0], zoom_start=11, width=400, height=400)

# ...with squares...
for _, xi in x.iterrows():
    folium.GeoJson(geo_json(xi['lat'], xi['lon'], xi['value'], step),
                   lambda x: x['properties']).add_to(m)

# ...and the original points
for elt in list(zip(df.lat, df.lon, df.value)):
    folium.Circle(elt[:2], color="white", radius=elt[2]).add_to(m)

m

Output:

---

Update (2):

Here's a version with interpolation on the grid using griddata:

import pandas as pd
import numpy as np
import folium
from scipy.interpolate import griddata

# parameters
n = 250                     # number of points
lat0 = 40.7
lon0 = -73.9
eps = 0.1
v_min, v_max = 0, 100       # min, max values

# generating values
lat = np.random.normal(lat0, eps, n)
lon = np.random.normal(lon0, eps, n)
value = numpy.random.uniform(v_min, v_max, n)

# set up the grid
step = 0.02
xi, yi = np.meshgrid(
    np.arange(lat.min() - step/2, lat.max() + step/2, step),
    np.arange(lon.min() - step/2, lon.max() + step/2, step),
)

# interpolate and normalize values
zi = griddata((lat, lon), value, (xi, yi), method='linear')
zi /= np.nanmax(zi)
g = np.stack([
    xi.flatten(),
    yi.flatten(),
    zi.flatten(),
], axis=1)

# geo_json returns a single square
def geo_json(lat, lon, value, step):
    cmap = mpl.cm.RdBu
    return {
      "type": "FeatureCollection",
      "features": [
        {
          "type": "Feature",
          "properties": {
            'color': 'white',
            'weight': 1,
            'fillColor': mpl.colors.to_hex(cmap(value)),
            'fillOpacity': 0.5,
          },
          "geometry": {
            "type": "Polygon",
            "coordinates": [[
                [lon - step/2, lat - step/2],
                [lon - step/2, lat + step/2],
                [lon + step/2, lat + step/2],
                [lon + step/2, lat - step/2],
                [lon - step/2, lat - step/2],
              ]]}}]}


# generating a map...
m = folium.Map(location=[lat0, lon0], zoom_start=9, width=400, height=400)

# ...with squares...
for gi in g:
    if ~np.isnan(gi[2]):
        folium.GeoJson(geo_json(gi[0], gi[1], gi[2], step),
                       lambda x: x['properties']).add_to(m)

# ...and the original points
for elt in list(zip(lat, lon, value)):
    folium.Circle(elt[:2], color='white', radius=elt[2]).add_to(m)

m

Output:

Answer 2

I appears to me that you need to filter your data so you split it into groups according to given categories. With those sets of points, you should then be able to generate convex hulls. It appears there are methods to do this in scipy - see here for some examples: Convex hull area in Python?