I was looking at the code of numpy.argmax function. I am confused which data structure numpy maintains for the argmax function.
https://numpy.org/doc/stable/reference/generated/numpy.argmax.html
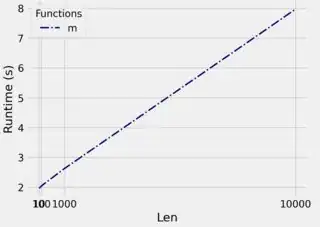
Eventually, I want to know what is the theoretical average case running time complexity of numpy argmax function for primitive data types. Is it O(logN) or O(N) in the average case?
This may be a relevant question as well: Faster alternatives to numpy.argmax/argmin which is slow
Thanks in advance.