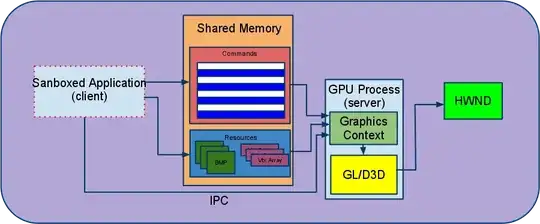
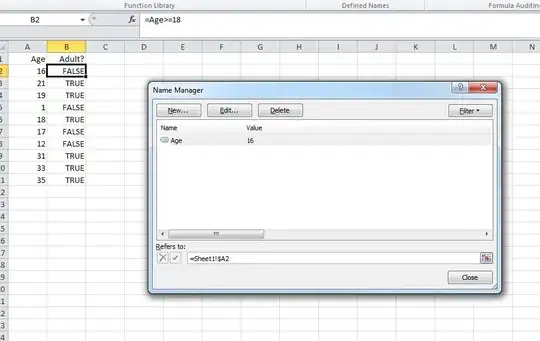
The first step is to find the angle of the line between the chosen point and the circle center with the x-axis. This angle is theta = atan2(y0-yc, x0-xc). Subtracting the starting angle and finding the fraction relative to the 2*pi of a complete circle gives the index: floor(theta * num_segments / (2 * pi)). This number has to be taken modulo the number of segments to obtain an index between 0 <= ind < num_segments.
To find the distance between the point and the circle, first calculate the distance to the center and subtract it from the radius. So, radius - sqrt((x0-xc)*(x0-xc)+(y0-yc)*(y0-yc)).
Here is some python code to illustrate the concept (avoiding numpy which would make things easier to implement, but harder to convert to other programming languages).
from matplotlib import pyplot as plt
from math import sin, cos, pi, atan2, floor
def draw_segmented_circle(xc, yc, radius, num_segments=8, theta0=0, selected_segment=None, **kwargs):
xpos = [xc + radius * cos(theta0 + 2 * pi * i / num_segments) for i in range(num_segments + 1)]
ypos = [xc + radius * sin(theta0 + 2 * pi * i / num_segments) for i in range(num_segments + 1)]
if selected_segment is not None:
i = selected_segment
plt.plot([xpos[i], xpos[i + 1]], [ypos[i], ypos[i + 1]], **kwargs)
else:
for i in range(num_segments):
plt.plot([xpos[i], xpos[i + 1]], [ypos[i], ypos[i + 1]], **kwargs)
plt.plot([xc, xpos[i]], [yc, ypos[i]], ls=':', **kwargs)
def find_closest_segment(x0, y0, xc, yc, radius, num_segments=8, theta0=0):
theta = (atan2(y0 - yc, x0 - xc) - theta0)
return (floor(theta * num_segments / (2 * pi)) + num_segments) % num_segments
xc, yc, radius, num_segments, theta0 = 0, 0, 5, 8, 0
circle = (xc, yc, radius, num_segments, theta0)
draw_segmented_circle(*circle, color='blue')
x0, y0 = 1, 3
ind = find_closest_segment(x0, y0, *circle)
draw_segmented_circle(*circle, selected_segment=ind, color='red')
plt.plot(x0, y0, 'o', color='red')
plt.gca().set_aspect('equal')
plt.show()