0

I am trying to get an exponential of a sum from the product of exponentials using SymPy. It seems to work for any base, but e (Euler number).

Example of code with a generic base for the exponential:

from sympy import symbols, Function
from sympy import Product, E, pi, exp
i,n,base=symbols('i n base')
f=Function('f')
P=Product(base**f(i),(i,1,n))
P.doit()

P is the following expression:

and after applying doit(), it becames:

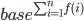
This code works for any base. I tested it with a number (eg.3.0), a variable (eg. x,base) or a constant defined in SymPy (eg. pi). Just when base=euler number, the doit() does not work.

P=Product(E**f(i),(i,1,n))
P.doit()

or

P=Product(exp(f(i)),(i,1,n))
P.doit()

the result is still:

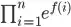and not

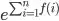
A work around could be to subs e with a variable like base and to make the opposite substitution at the end.

But is there any better solution?

Versions: python 3.7.4, SymPy 1.4

Fabrizio
  • 91
  • 1
  • 6

1 Answers1

2

I guess this works for the other cases but not exp because E**x is an instance of the class exp rather than Pow. Probably the sympy code can be made consistent by checking for both classes.

You can use rewrite to convert between Products and Sums using exp and log:

In [47]: P = Product(E**f(i), (i, 1, n))                                                                                                                      

In [48]: P                                                                                                                                                    
Out[48]: 
  n         
─┬──┬─      
 │  │   f(i)
 │  │  ℯ    
 │  │       
i = 1       

In [49]: P.rewrite(Sum)                                                                                                                                       
Out[49]: 
   n       
  ___      
  ╲        
   ╲       
   ╱   f(i)
  ╱        
  ‾‾‾      
 i = 1     
ℯ
Oscar Benjamin
  • 12,649
  • 1
  • 12
  • 14