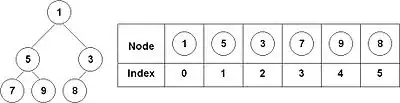
Often we need trees in algorithms and I get out a tree with lots of pointers and recursion.
Sometimes I need more speed an I put the tree into an 2D array like so:
Example of a binary tree stored in an array
+-----------------+
|0eeeeeeeeeeeeeeee| //no pointers needed, parent/child, is y dimension,
|11 dddddddd| //sibbling is x dimension of the array.
|2222 cccc| //The 123 tree is stored root up.
|33333333 bb| //Notice how the abc-tree is stored upside down
|4444444444444444a| //The wasted space in the middle, is offset by the fact
+-----------------+ //that you do not need up, down, and sibbling pointers.
I love this structure because it allowes me speed up options that I don't have when using pointers and recursion.
But notice that wasted space in the middle....
How do I get rid of/reuse that wasted space?
Requirements
I only use this structure if I need every last bit of speed, so a solution with lots of translations and address calculations to get to that space will not be helpful.