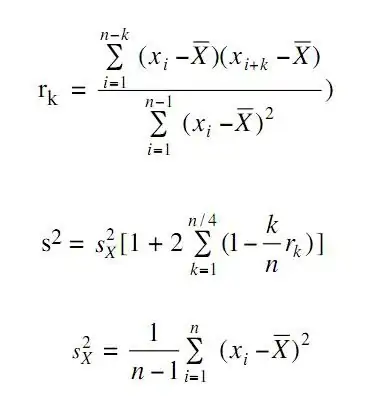Finding the largest area under a curve | pandas, matplotlib

Question

I am struggling a bit in this one - in order to find the necessary battery capacity I need to analyze production/demand over a year's worth of data. To do this, I figured I need to calculate the biggest area under the 0 line. I guess I need to find the start/end points of that area and multiply everything by its respective y-value?

Here is a shortened version of the graph I have: That is the biggest area under the 0 in the image, but in the full dataset it could be any area. I know how to integrate it in the case I find the boundaries of the area in question but I'm struggling to find an efficient way to do that.

My dataframe looks like this:

                     demand  Production    diff
Time
2019-01-01 00:15:01   17.25      32.907  15.657
2019-01-01 00:30:01   17.80      32.954  15.154
...                     ...         ...     ...
2019-01-16 22:15:02   17.34      27.704  10.364
2019-01-16 22:30:01   18.67      35.494  16.824

I use this snippet to find the length in timesteps of the longest area but I'm missing if there's a way to multiply the points by their y-values (diff). It's technically not correct, however, considering that an area might be long but narrow and another might be shorter and taller, so with an overall bigger area.

def max0(sr):
     return (sr >= 0).cumsum().value_counts().max() - (0 if (sr >= 0).cumsum().value_counts().idxmax() < 0 else 1)

Answer 1

You can find the largest area under the 0-line. I generated my own data

x = np.random.randn(100000)
x = x.cumsum()-x.mean()
plt.plot(x);

Now calculate the start and end points for positive and negative sequences. Every value in a sequence gets an increasing integer to be able to group by sequence.

x1 = np.diff(x < 0).cumsum()

Use pandas groupby to compute all areas and find the largest negative

df = pd.DataFrame({
    'value': x[1:],
    'border': x1
})
dfg = df.groupby('border')
mingr = dfg.apply(lambda x: np.trapz(x.value)).idxmin()
plt.plot(x[1:])
plt.plot(
    dfg.get_group(mingr).value
);
plt.title(
    "position from {} to {}".format(
        dfg.get_group(mingr).index[0],
        dfg.get_group(mingr).index[-1]));

How this works

I create a dataset that is easier to follow along

x = np.array([3,4,4.5,3,2])
X = np.r_[x,-x,x,-x]+np.random.normal(0,.2,20)
plt.figure(figsize=(12,5))
plt.axhline(0, color='gray')
plt.plot(X, 'o--');

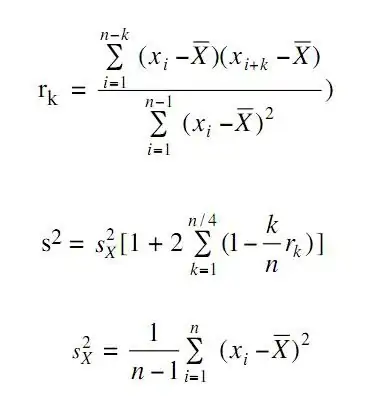
I want to know the sequences with consecutive negative or positive values. This can be archived with the filter X < 0.

df = pd.DataFrame({'value': X, 'lt_zero': X < 0})
df[:10]
      value  lt_zero
0  3.125986    False
1  3.885588    False
2  4.580410    False
3  2.998920    False
4  1.913088    False
5 -2.902447     True
6 -3.986654     True
7 -4.373026     True
8 -2.878661     True
9 -1.929964     True

Now I can find the indices where the sign changes, when I diff every consecutive value. I concat one False before the data to not loose the first value.

df['sign_switch'] = np.diff(np.r_[False, X < 0])
df[:10]
      value  lt_zero  sign_switch
0  3.125986    False        False
1  3.885588    False        False
2  4.580410    False        False
3  2.998920    False        False
4  1.913088    False        False
5 -2.902447     True         True
6 -3.986654     True        False
7 -4.373026     True        False
8 -2.878661     True        False
9 -1.929964     True        False

With cumsum() I get for every sequence an increasing integer value. Now I have a grouping variable for every sequence.

df['sign_sequence'] = np.diff(np.r_[False, X < 0]).cumsum()
df[:10]
      value  lt_zero  sign_switch  sign_sequence
0  3.125986    False        False              0
1  3.885588    False        False              0
2  4.580410    False        False              0
3  2.998920    False        False              0
4  1.913088    False        False              0
5 -2.902447     True         True              1
6 -3.986654     True        False              1
7 -4.373026     True        False              1
8 -2.878661     True        False              1
9 -1.929964     True        False              1

For every group I can compute the integral for the values in the group.

sign_groups = df.groupby('sign_sequence')
sign_groups.apply(lambda x: np.trapz(x.value))
sign_sequence
0    13.984455
1   -13.654547
2    14.370044
3   -14.549090

You can access every group later and use the areas. For example to plot the areas.

plt.figure(figsize=(12,5))
plt.plot(X,'o--')
plt.axhline(0, c='gray')
for e,group in enumerate(sign_groups):
    plt.fill_between(group[1].index,0, group[1].value)
    area = np.trapz(group[1].value)
    plt.text((e)*5+1.5, np.sign(area) * 1.25, f'{area:.2f}', fontsize=12)