Poincaré Embeddings
However, while complex symbolic datasets often exhibit a latent hierarchical structure, state-of-the-art methods typically learn embeddings in Euclidean vector spaces, which do not account for this property. For this purpose, we introduce a new approach for learning hierarchical representations of symbolic data by embedding them into hyperbolic space – or more precisely into an n-dimensional Poincaré ball.
Poincaré embeddings allow you to create hierarchical embeddings in a non-euclidean space. The vectors on the outside of the Poincaré ball are lower in hierarchy compared to the ones in the center.

The transformation to map a Euclidean metric tensor to a Riemannian metric tensor is an open d-dimensional unit ball.
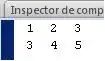
Distances between 2 vectors in this non-euclidean space are calculated as
The research paper for Poincaré embeddings is wonderfully written and you will find some wonderful implementations in popular libraries for them as well. Needless to say, they are under-rated.
Two implementations that you can use are found in -
tensorflow_addons.PoincareNormalizegensim.models.poincare
Tensorflow Addons implementation
According to the documentation, for a 1D tensor, tfa.layers.PoincareNormalize computes the following output along axis=0.
(x * (1 - epsilon)) / ||x|| if ||x|| > 1 - epsilon
output =
x otherwise
For a higher dimensional tensor, it independently normalizes each 1-D slice along the dimension axis.
This transformation can be simply applied to an embedding of n-dims. Let's create a 5 dim embedding for each element of the time series. The dimension axis=-1 in this case, which is mapped from a euclidean space to a non-euclidean space.
from tensorflow.keras import layers, Model, utils
import tensorflow_addons as tfa
X = np.random.random((100,10))
y = np.random.random((100,))
inp = layers.Input((10,))
x = layers.Embedding(500, 5)(inp)
x = tfa.layers.PoincareNormalize(axis=-1)(x) #<-------
x = layers.Flatten()(x)
out = layers.Dense(1)(x)
model = Model(inp, out)
model.compile(optimizer='adam', loss='binary_crossentropy')
utils.plot_model(model, show_shapes=True, show_layer_names=False)
model.fit(X, y, epochs=3)
Epoch 1/3
4/4 [==============================] - 0s 2ms/step - loss: 7.9455
Epoch 2/3
4/4 [==============================] - 0s 2ms/step - loss: 7.5753
Epoch 3/3
4/4 [==============================] - 0s 2ms/step - loss: 7.2429
<tensorflow.python.keras.callbacks.History at 0x7fbb14595310>
Gensim implementation
Another implementation Poincare embeddings can be found in Gensim. Its very similar to what you would use when working with Word2Vec from Gensim.
The process would be -
- Train Gensim embeddings (word2vec or poincare)
- Initialize Embedding layer in Keras with embeddings
- Set the embedding layer as non-trainable
- Train model for the downstream task
from gensim.models.poincare import PoincareModel
relations = [('kangaroo', 'marsupial'), ('kangaroo', 'mammal'), ('gib', 'cat'), ('cow', 'mammal'), ('cat','pet')]
model = PoincareModel(relations, size = 2, negative = 2) #Change size for higher dims
model.train(epochs=10)
print('kangroo vs marsupial:',model.kv.similarity('kangaroo','marsupial'))
print('gib vs mammal:', model.kv.similarity('gib','mammal'))
print('Embedding for Cat: ', model.kv['cat'])
kangroo vs marsupial: 0.9481239343527523
gib vs mammal: 0.5325816385250299
Embedding for Cat: [0.22193988 0.0776986 ]
More details on training and saving Poincare embeddings can be found here.


