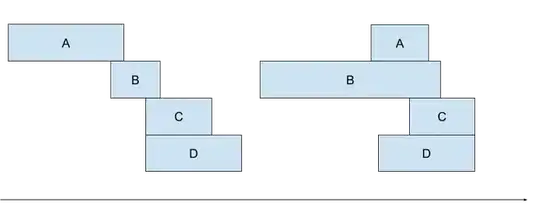
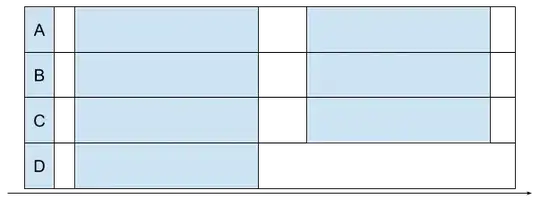
Below is my solution implemented in Java. It's similarly to Dave's approach a sweep line algorithm.
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
public class IntervalSolver {
public static void main(String []args){
ArrayList<Interval> intervals = new ArrayList<>();
final int A = 0;
final int B = 1;
final int C = 2;
final int D = 3;
// intervals.add(new Interval(1, 10, A));
// intervals.add(new Interval(9, 12, B));
// intervals.add(new Interval(11, 15, C));
// intervals.add(new Interval(11, 18, D));
// intervals.add(new Interval(26, 29, A));
// intervals.add(new Interval(20, 30, B));
// intervals.add(new Interval(28, 33, C));
// intervals.add(new Interval(27, 33, D));
// intervals.add(new Interval(1, 10, A));
// intervals.add(new Interval(1, 10, B));
// intervals.add(new Interval(1, 10, C));
// intervals.add(new Interval(1, 10, D));
// intervals.add(new Interval(16, 25, A));
// intervals.add(new Interval(16, 25, B));
// intervals.add(new Interval(16, 25, C));
intervals.add(new Interval(1, 7, A));
intervals.add(new Interval(1, 10, B));
intervals.add(new Interval(1, 10, C));
intervals.add(new Interval(1, 10, D));
compute(intervals, 4);
}
public static class Interval {
public int start;
public int end;
public int entity;
public Interval(int start, int end, int entity) {
this.start = start;
this.end = end;
this.entity = entity;
}
}
public static class Point implements Comparable<Point> {
boolean start;
public Interval interval;
public int pos() {
return start ? interval.start : interval.end;
}
public Point(Interval interval, boolean start) {
this.interval = interval;
this.start = start;
}
@Override
public int compareTo(Point other) {
int diff = pos() - other.pos();
if (diff != 0)
return diff;
return (start ? 0 : 1) - (other.start ? 0 : 1);
}
}
public static class Solution {
public Interval[] intervals;
public Solution(Interval[] intervals) {
this.intervals = intervals;
}
public int value() {
int value = 0;
for (int i = 0; i < intervals.length; i++)
value += intervals[i] != null ? 1 : 0;
return value;
}
@Override
public boolean equals(Object other) {
Solution s = (Solution)other;
if (s.intervals.length != intervals.length)
return false;
for (int i = 0; i < intervals.length; i++)
if ((intervals[i] == null && s.intervals[i] != null) || (intervals[i] != null && s.intervals[i] == null))
return false;
return true;
}
@Override
public int hashCode() {
int hashCode = 0;
for (int i = 0; i < intervals.length; i++)
hashCode = hashCode << 1 | (intervals[i] != null ? 1 : 0);
return hashCode;
}
@Override
public String toString() {
var sb = new StringBuilder();
sb.append('[');
for (int i = 0; i < intervals.length; i++) {
sb.append(intervals[i] != null ? '1' : '0');
if (i < intervals.length - 1)
sb.append(',');
}
sb.append(']');
return sb.toString();
}
}
public static void compute(List<Interval> series, int entities) {
ArrayList<Point> points = new ArrayList<>();
for (var i : series) {
points.add(new Point(i, true));
points.add(new Point(i, false));
}
points.sort(null);
HashMap<Solution, Integer> solutions = new HashMap<>();
Interval[] currentIntervals = new Interval[entities];
for (int i = 0; i < points.size(); i++) {
var p = points.get(i);
if (p.start)
currentIntervals[p.interval.entity] = p.interval;
else
currentIntervals[p.interval.entity] = null;
if (i < points.size() - 1 && p.pos() == points.get(i + 1).pos())
continue;
var copy = new Solution(currentIntervals.clone());
int count = solutions.getOrDefault(copy, 0);
solutions.put(copy, count + 1);
}
long maxValue = 0;
Solution best = null;
for (var entry : solutions.entrySet()) {
var solution = entry.getKey();
var count = entry.getValue();
if (count == 1)
continue;
long value = solution.value();
if (value > maxValue) {
maxValue = value;
best = solution;
}
}
// extra intersections:
for (var entry : solutions.entrySet()) {
var solution = entry.getKey();
var count = entry.getValue();
if (count > 1)
continue;
long value = solution.value();
if (value <= maxValue)
continue;
for (var innerEntry : solutions.entrySet()) {
var innerSolution = innerEntry.getKey();
var innerCount = innerEntry.getValue();
if (solution == innerSolution || innerCount > 1)
continue;
long innerValue = innerSolution.value();
if (innerValue <= maxValue)
continue;
var merge = new Solution(solution.intervals.clone());
for (int i = 0; i < entities; i++) {
var int1 = solution.intervals[i];
var int2 = innerSolution.intervals[i];
if (int2 == null || int1 == int2)
merge.intervals[i] = null;
}
long mergeValue = merge.value();
if (mergeValue > maxValue) {
maxValue = mergeValue;
best = merge;
}
}
}
System.out.println("Best: " + best);
}
}
It prints Best: [false, true, true, true] which means BCD.
It could be easily extended to print the exact coordinates where the intersection occurs.
It's complexity is O(n*lg n + nk) where n is the number of intervals and k is the number of entities. If k = O(n), then the whole complexity becomes O(n^2).
Edit:
Changed the behaviour to account for the update in the requirements from the OP. The idea is based on taking each pair of potential solutions which occur only once and intersecting them. Their intersection by definition occurs at least twice. If it's value is larger than the current best it becomes the new result. The complexity has risen to O(n*lg n + n^2*k) where n is the number of intervals and k is the number of entities. If k = O(n), then the whole complexity becomes O(n^3).
Edit2:
Fixed the code for extra intersections, by adding the requirement that the intervals for the same entity must be distinct.