I'm not completely certain I've understood what you're looking for, but from the second question it looks like you are looking for all cross-combinations of columns within a data.frame.
Disclaimer: The two answers already provided are more readable, where I focus on speed.
As you are performing what is often known as a cross-join (or outer-full-join) one aspect that quickly becomes a concern as n increases is efficiency. For efficiency it helps to split the problem into smaller sub-problems, and find a solution for each problem. As we need to find all unique combinations within the set of columns including the null set (value = NA), we can reduce this problem into 2 sub-problems.
- Find unique values for each column including the null set
- Expand this set to include all combinations of each column.
Using this idea we can quickly concoct a simple solution using expand.grid, unique and lapply. The only tricky part is to include the null set, but we can do this by selecting NA row from the data.frame including all rows.
# Create null-set-included data.frame
nullset_df <- plusminus_df[c(NA, seq_len(nrow(plusminus_df))), ]
# Find all unique elements, including null set
unique_df <- lapply(nullset_df, unique)
# Combine all unique sets
expand.grid(unique_df)
or as a function
nullgrid.expand <- function(df, ...)
expand.grid(lapply(df[c(NA, seq_len(nrow(df))), ], unique), ...)
This is fairly fast (benchmarks and performance graphs later), but I wanted to go one step further. The data.table package is known for it's high-performance functions, and one of those functions in the CJ function, for performing cross-joins. Below is one implementation using CJ
library(data.table)
nullgrid.expand.dt <- function(df, ...)
do.call(CJ, args = c(as.list(df[c(NA, seq_len(nrow(df))), ]),
sorted = FALSE,
unique = TRUE))
The function requires vector input, forcing one to use do.call (or similar) which makes the function slightly less readable. But is there any performance gain? To test this, I ran a microbenchmark on the two functions and the ones provided by the existing answers (code below), the result is visualized in a violin plot below:
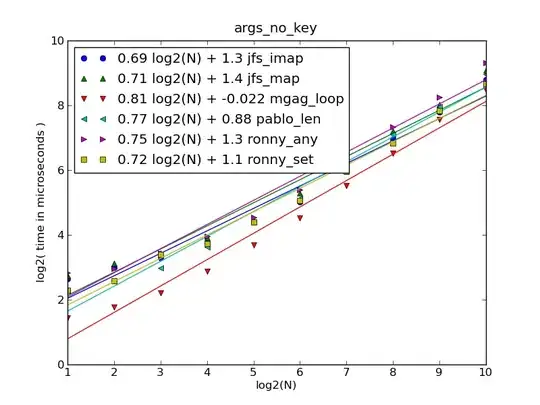
From the plot it is quite clear that @pauls answer outperforms @ekoam's answer, but the two functions above both outperform the provided answers in terms of speed. But the question said that the input might have any number of dimension, so there is also the question of how well our function scales with the number of columns and the number of unique values (here we only have "+" and "-" but what if we had more?). For this I reran the benchmark for n_columns = 3, 4, ..., 10 and n_values = 2, 4, ... 10. The 2 results are visualized with smooth curves below.
First we'll visualize the time as a function of number of columns. Note that the y axis is on logarithmic scale (base 10) for easier comparison.
From the visualization it is quite clear that, with increasing number of columns, the choice of method becomes very important. The suggestion by @ekoam becomes very slow, primarily because it delays a call to unique till the very end. The remaining 3 methods are all much faster, while nullgrid.expand.dt becomes more than 10 times faster in comparison to the remaining methods once we get more than 8 columns of data.
Next lets look at the timing compared to the number of values in each column (n-columns fixed at 5)

Again we see a similar picture. Except for a single possible outlier for nullgrid.expand, which seems to become slower than the answer by paul as the number of unique values increase, we see that nullgrid.expand.dt remains faster, although here it seems to only be saving (exp(4) - exp(3.6)) / exp(3.6) ~ 50 % (or twice as fast) compared to paul's answer by the time we reach 10 unique values.
Please note that I did not have enough RAM to run the benchmark for number of unique values or columns greater than the ones shown.
Conclusion
We've seen that there are many ways to reach the answer sought by the question, but as the number of columns and unique values increase the choice of method becomes more and more important. By utilizing optimized libraries, we can drastically reduce the time required to get the cross-join of all column values, with only minimal effort. With extended effort using Rcpp we could likely reduce the time complexity even further, while this is outside the scope of my answer.
Benchmark code
# Setup:
set.seed(1234)
library(tidyverse)
library(data.table)
nullgrid.expand <- function(df, ...)
expand.grid(lapply(df[c(NA, seq_len(nrow(df))), ], unique), ...)
nullgrid.expand.dt <- function(df, ...)
do.call(CJ, args = c(as.list(df[c(NA, seq_len(nrow(df))), ]),
sorted = FALSE,
unique = TRUE))
markers=LETTERS[1:5]
plusminus_df <- expand.grid(lapply(seq(markers), function(x) c("+","-")), stringsAsFactors=FALSE)
names(plusminus_df)=LETTERS[1:5]
bm <- microbenchmark(
nullgrid.expand = nullgrid.expand(plusminus_df),
nullgrid.expand.dt = nullgrid.expand.dt(plusminus_df),
ekoam = unique(bind_rows(apply(
plusminus_df, 1L,
function(r) head(expand.grid(lapply(r, c, NA_character_), stringsAsFactors = FALSE), -1L)
))),
paul = {
plusminus_df %>%
add_row() %>%
map(unique) %>%
expand.grid()
},
control = list(warmup = 5)
)
library(ggplot2)
autoplot(bm) + ggtitle('comparison between cross-join')
Timing function
time_function <- function(n = 5, j = 2){
idx <- seq_len(n)
df <- do.call(CJ, args = c(lapply(idx, function(x) as.character(seq_len(j))),
sorted = FALSE,
unique = TRUE))
names(df) <- as.character(idx)
microbenchmark(
nullgrid.expand = nullgrid.expand(df),
nullgrid.expand.dt = nullgrid.expand.dt(df),
ekoam = unique(bind_rows(apply(
df, 1L,
function(r) head(expand.grid(lapply(r, c, NA_character_), stringsAsFactors = FALSE), -1L)
))),
paul = {
df %>%
add_row() %>%
map(unique) %>%
expand.grid()
},
times = 10,
control = list(warmup = 5)
)
}
res <- lapply(seq(3, 10), time_function)
for(i in seq_along(res)){
res[[i]]$n <- seq(3, 10)[i]
}
ggplot(rbindlist(res), aes(x = n, y = log(time / 10^4, base = 10), col = expr)) +
geom_smooth(se = FALSE) +
ggtitle('time-comparison given number of columns') +
labs(y = 'log(ms)', x = 'n')
ggsave('so_2.png')
res <- lapply(c(seq(2, 10, 2)), time_function, n = 5)
for(i in seq_along(res)){
res[[i]]$n <- seq(2, 10, 2)[i]
}
ggplot(rbindlist(res), aes(x = n, y = log(time / 10^4, base = 10), col = expr)) +
geom_smooth(se = FALSE) +
ggtitle('time-comparison given number of unique values') +
labs(y = 'log(ms)', x = 'n unique values per column')
ggsave('so_3.png')


