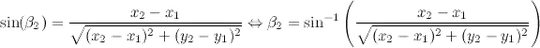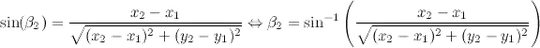I have a the following data:
starting_point = 0.00000016
mean = 0.000351
end_point = 0.75
Is it correct to use this to determine the skew?
from scipy.stats import skew
skew([0.00000016, 0.000351, 0.75])
>> 0.7071062587209218
How can I plot a distribution to show the skewed distribution in python 3?
You have calculated the skewness of the three datapoints. As two are rather small compared to the third the skewness is positive. Its trickier to fit a distribution through data (especially just three points). You can refer to fitting empirical distributions for an exhaustive description.
Just as an example of how a distribution might look like which is skewed (as your data suggests; I have chosen a gamma-distribution - careful: the actual fitting is much more complicated, refer to the answer above; this is just to show the difference):
from scipy import stats
import numpy as np
import matplotlib.pyplot as plt
starting_point = 0.00000016
mean = 0.000351
end_point = 0.75
data = [starting_point, mean, end_point]
print('skewness of data:', skew(data))
a, loc, scl = stats.gamma.fit(data)
x = np.arange(starting_point, end_point, 0.0002635)
plt.plot(x, stats.gamma.pdf(x, a, loc, scl))
plt.show()
dvals = [val for val in stats.gamma.pdf(x, a, loc, scl)]
print('skewness of distribution:', skew(dvals))
will result in a different skewness (taking your mean and starting- and end-points to determine the distribution). This gives
skewness of data: 0.7071062587209218
skewness of distribution: 53.32916979819496
