How to prevent deep branch of an n-ary tree using tree rotation?

Question

I am trying to imagine a tree sort of system where you have tree nodes which can have powers of 2 nodes up to 32 nodes each. The data is stored in "leaves", and the leaves are bundled into power of 2 up to 32 nodes likewise. What I'm thinking is that upon insert, if the leaf node is 32 nodes, then you split it in half, add those two halves to a new parent, and add that to the tree. The problem is, if you keep inserting in the same place, I could see this sort of tree emerging, where it splits the same sort of place over and over again, resulting in a deep branch, as each leaf reaches 32 items.

If each of those leaf nodes represents up to 32 items each, and each internal container node can contain up to 32 sub-containers/leaves each, how can I use rotation to balance this tree? The problem is I don't know how the final tree would look, so I don't know how the rotation should work. I try to imagine it but don't get there.

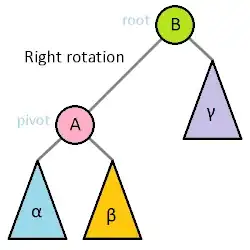
Animated tree rotations are all pretty basic and don't show how to do it on non-binary trees.

Since the nodes could have up to 32 nodes, a deeply nested tree should end up looking something like this (say the first layer I actually drew 32 nodes, so it was full):

I'm not sure exactly what it should look like, which is the reason for this question. But as you insert nodes in the tree, the thing should somehow rotate so it doesn't get long branches like the ones above, yet each node can have up to 32 children (or objects/items if they are the leaf type). Is this at all possible? If so, what is some JavaScript for how to implement the rotation to keep this n-ary tree "balanced" like a BST?

Sidenote. I am trying to tinker with a rotation scheme, but not getting very far.

// split()
// rotate() // shift

const createTree = () => createTreeLeaf()

const createTreeContainer = () => {
  return {
    type: 'container',
    list: [],
    size: 0
  }
}

const createTreeLeaf = () => {
  return {
    type: 'leaf',
    list: [],
    size: 0
  }
}

const insertAt = (tree, index, item) => {
  if (tree.size == 0) {
    tree.list.push(item)
    tree.size++
    return tree
  }
  let nodes = [tree]
  let startSize = 0
  a:
  while (true) {
    b:
    for (let i = 0, n = nodes.length; i < n; i++) {
      let node = nodes[i]
      let endSize = startSize + node.size

      if (startSize <= index && index < endSize) {
        // it's within here.
        if (node.type == 'container') {
          nodes = node.list
          break b
        } else {
          let relativeIndex = index - startSize
          // grow if less than max
          if (node.size == 32) {
            const firstHalf = node.list.splice(0, 16)
            const secondHalf = node.list.splice(-16)
            const container = createTreeContainer()
            const aNode = createTreeLeaf()
            aNode.list.push(...firstHalf)
            aNode.size = 16
            const bNode = createTreeLeaf()
            bNode.list.push(...secondHalf)
            bNode.size = 16
            container.list.push(aNode, bNode)
            container.size = 32
            container.parent = node.parent
            node.type = container.type
            node.list = container.list
            node.size = container.size
            i--
            continue
          } else if (node.size && relativeIndex > node.size - 1) {
            let newArray = new Array(node.size * 2)
            node.list.forEach((x, i) => newArray[i] = x)
            node.list = newArray
          }
          let j = node.size
          while (j > relativeIndex) {
            node.list[j] = node.list[j - 1]
            j--
          }
          node.list[relativeIndex] = item
          node.size++
          break a
        }
      }
    }
  }
}

let tree = createTree()

for (let i = 1, n = 2000; i <= n; i++) {
  insertAt(tree, 0, i)
}
console.log(JSON.stringify(tree))

Currently ending up with a deep tree, not sure how to implement this rotation.

If there is an alternative to using rotation as well that will create a balanced tree, that would also be a suitable answer.

Answer 1

What you are trying to do is the same as self-balancing binary search trees but not limited to just max 2 children. You can directly take help from B-Tree or B+ Tree.

B-Tree Insertion says

All insertions start at a leaf node. To insert a new element, search the tree to find the leaf node where the new element should be added. Insert the new element into that node with the following steps:

1. If the node contains fewer than the maximum allowed number of elements, then there is room for the new element. Insert the new element in the node, keeping the node's elements ordered.

2. Otherwise the node is full, evenly split it into two nodes so:

   1. A single median is chosen from among the leaf's elements and the new element.
   2. Values less than the median are put in the new left node and values greater than the median are put in the new right node, with the median acting as a separation value.
   3. The separation value is inserted in the node's parent, which may cause it to be split, and so on. If the node has no parent (i.e., the node was the root), create a new root above this node (increasing the height of the tree).

This shows how to split instead of rotating the trees.

---

Above excerpt related to B-Tree insertion is kind of a pseudo-code/broad steps in the algorithm. Instead of adding more of pseudo-code, let me take a simulation from here that explains the insert operation. The same link also has the code.

Let us understand the algorithm with an example tree having max 3 children and the same node can hold 5 keys. Consider a sequence of integers 10, 20, 30, 40, 50, 60, 70, 80 and 90 in an initially empty B-Tree.

Initially root is NULL. Let us first insert 10.

Let us now insert 20, 30, 40 and 50. They all will be inserted in root because the maximum number of keys a node can accommodate is is 5.

Let us now insert 60. Since root node is full, it will first split into two, then 60 will be inserted into the appropriate child.

Let us now insert 70 and 80. These new keys will be inserted into the appropriate leaf without any split.

Let us now insert 90. This insertion will cause a split. The middle key will go up to the parent.

I hope this helped!

---

Feel free to play around with this B-Tree Visualization!

---

Not to mention, you can always find javascript implementations of B-Tree on the internet e.g. this one.