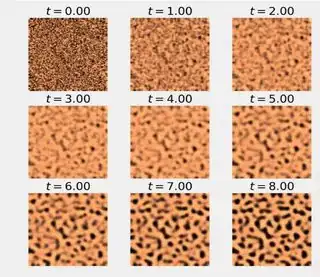
I'm trying to implement the model described in this paper, which simulates the equation proposed by Alan Turing of the FitzHugh-Nagumo model in 2D as a model for forming animal skin patterns — in other words: simulating two substances diffusing across a surface, how they interact with each other, and what patterns arise. This is the paper's result:
I've implemented it (my interpretation of at least) in Processing/Java, but it's not working like it should (values are diverging lots, even by the first iteration), so I'm wondering what's going wrong in my implementation (included at the end of the post).
These are the 3 relevant parts from the paper regarding implementation:
1. U & V
There are two substances, u and v (which can be thought of as an activator and inhibitor respectively)
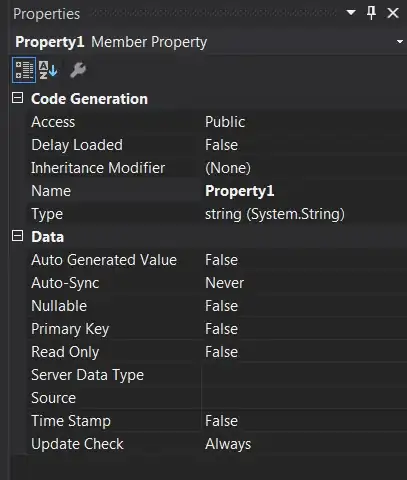
2. Finite difference equations
A fairly simple pixel convolution is defined for each value (pixel) of u and v. Values for a given pixel on the next generation are calculated using both it and its neighbours' current-iteration values.
The value of u on the n+1 iteration for a given pixel (i,j) is defined as:
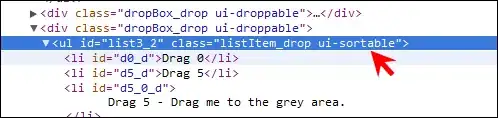
The value of v on the n+1 iteration for a given pixel (i,j) is defined as:
3. Constants they used
So the problem I'm getting is that the values of u and v are quickly diverging to infinity/NaN (I expect they should stay within 0...1 although the paper doesn't explicitly mention this). v seems to diverge first, taking u along with it, as can be seen here (for some constant index):
0.94296926 0.77225316 // u, v after random initialisation
0.91600573 -62633.082 // values after first iteration -- v has already diverged massively
63.525314 5.19890688E8 // second iteration -- even more divergence
-520088.38 -2.98866172E14 // ...and so on...
1.40978577E14 1.2764294E19
-Infinity -1.7436987E24
NaN NaN
NaN NaN
Code
//Parallel Simulation of Pattern formation in a reactiondiffusion system of Fitzhugh-Nagumo Using GPU CUDA
// Alfredo Gormantara and Pranowo1
static final float a = 2.8e-4;
static final float b = 5.0e-3;
static final float k = -0.005;
static final float tau = 0.1;
static final float delta_t = 1e-3;
float[][] u; // activator
float[][] v; // inhibitor
void setup() {
size(512, 512);
frameRate(5);
u = new float[height][width];
v = new float[height][width];
for (int i = 0; i < u.length; i++) {
for (int j = 0; j < u[0].length; j++) {
u[i][j] = random(1); // random of max of 1 ?
v[i][j] = random(1); // random of max 1?
}
}
loadPixels();
}
void draw() {
float[][] u_n_1 = new float[height][width]; // array holding the n+1 iteration values of u
float[][] v_n_1 = new float[height][width]; // array holding the n+1 iteration values of v
float denom = 2f / width; // 2/MESH_SIZE -- I think mesh_size is dimension of the grid
denom*=denom; // square for denominator
println(u[34][45], v[34][45]); // print vals of one location to see divergence
for (int y = 0; y < height; y++) {
int negative_y_i = y-1 < 0 ? height-1 : y-1; // wrap around grid
for (int x = 0; x < width; x++) {
final float u_n = u[y][x];
final float v_n = v[y][x];
int negative_x_i = x-1 < 0 ? width-1 : x-1; // wrap around grid
// calculate laplace (12)
float u_n_1_laplace = u[y][(x+1) % (width)] + u[y][negative_x_i] + u[(y+1) % (height)][x] + u[negative_y_i][x]; //n+1th iteration
u_n_1_laplace -= (4 * u_n);
u_n_1_laplace /= denom; // divide by (2/DIM)^2
u_n_1_laplace *= a;
// calculate n+1th iteration u value
u_n_1[y][x] = u_n + delta_t*( u_n_1_laplace + u_n -(u_n*u_n*u_n) - v_n + k );
// calculate laplace (14)
float v_n_1_laplace = v[y][(x+1)% (width)] + v[y][negative_x_i] + v[(y+1)% (height)][x] + v[negative_y_i][x]; //n+1th iteration
v_n_1_laplace -= (4 * u_n);
v_n_1_laplace /= denom; // denom is really small, so value goes huge
v_n_1_laplace *=b;
v_n_1[y][x] = v_n + (tau/delta_t)*( v_n_1_laplace + u_n - v_n);
pixels[y*width + x] = color((int) ((u_n_1[y][x]-v_n_1[y][x])*255));
}
}
u = u_n_1.clone(); // copy over new iteration values
v = v_n_1.clone(); // copy over new iteration values
updatePixels();
}