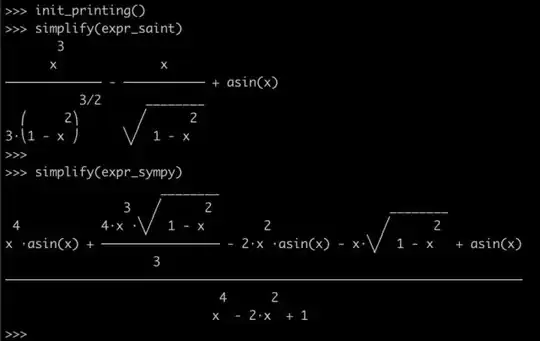How can I convince Sympy to come to the same simplification SAINT does for the 1961 MIT undergrad calculus problem?

Question

The program for James R Slagle's MIT thesis A heuristic program that solves symbolic integration problems in freshman calculus, symbolic automatic integrator (SAINT) is famous(ish) for being the first practical "expert system" symbolic integrator and able to solve all of the problems on the MIT Undergraduate Calculus test (pedantically, a couple were missed, but it could have solved them; detailed here in this excellent YouTube video)

His thesis is freely available here: https://dspace.mit.edu/handle/1721.1/11997

I was excited to try Sympy on this because it looked approachable and was a reasonably difficult simplification I happened to already have an answer to .. however, Sympy doesn't simplify the integral to such a good(subjective?) simplification as the 1961 program (though it does return an equivalent result!)

Question and Speculation

How can I convince Sympy to simplify to the same equation?
Why doesn't it come to the same, seemingly-simpler result?

Perhaps it chooses the first possible outcome, or tan**3 is determined to be worse? if so, why doesn't it simplify SAINT's output?)

Perhaps it sets off down a different branch when it finds some matching Fu-routine?

Exam problem 3c

Sympy simplification

from sympy import *
x = symbols("x", real=True)  # should this be assumed?
expr_inner = (x**4) / ((1 - x**2)**Rational(5,2))
expr_integral = integrate((expr_inner), x)
print(simplify(expr_integral))

(x**4*asin(x) + 4*x**3*sqrt(1 - x**2)/3 - 2*x**2*asin(x) - x*sqrt(1 - x**2) + asin(x))/(x**4 - 2*x**2 + 1)

Proof of Equality

from sympy import *
x = symbols("x", real=True)  # should this be assumed?
expr_saint = asin(x) + Rational(1,3)*tan(asin(x))**3 - tan(asin(x))
expr_sympy = (x**4*asin(x) + 4*x**3*sqrt(1 - x**2)/3 - 2*x**2*asin(x) - x*sqrt(1 - x**2) + asin(x))/(x**4 - 2*x**2 + 1)
expr_saint.equals(expr_sympy)  # alternatively simplify(expr_saint - expr_sympy) https://stackoverflow.com/a/37115190/

True

Equations Display

score 1 · Accepted Answer · answered Jan 10 '21 at 08:26

The main part is factoring out asin(x) and pulling it separate from the fraction. After this, sympy can prove the two expressions are equal:

from sympy import *
from IPython.display import Math, display
x = symbols("x", real=True)  # should this be assumed?
expr_saint = asin(x) + Rational(1,3)*tan(asin(x))**3 - tan(asin(x))
expr_sympy = (x**4*asin(x) + 4*x**3*sqrt(1 - x**2)/3 - 2*x**2*asin(x) - x*sqrt(1 - x**2) + asin(x))/(x**4 - 2*x**2 + 1)

r=[]
r.append(latex(expr_sympy))
expr_sympy = expr_sympy.collect(asin(x))
r.append(latex(expr_sympy))
expr_sympy = apart(expr_sympy,asin(x))
r.append(latex(expr_sympy))

display(Math(" \\Longrightarrow ".join(r)))

display(simplify(expr_saint - expr_sympy))

Output:

ti7 · Answer 2 · 2021-01-11T02:31:13.837

@wsdookadr gave me the missing simplification step; showing apart() can easily get asin(x) (which is obviously a common factor) out on its own, and so create a very similar, yet more simplified form than the SAINT output.

Thinking more along these lines, the SAINT output is not as simplified as it could be and so should be further simplified before comparing (to my knowledge, SAINT was not designed to continue simplifying once integrated)

first coercing the result to a single fraction with ratsimp() pushes Sympy to clean up the denominator (this combines the fractions)
calling apart() splits them back up, though they remain simplified

This gives a more expected match