python, smoothing 2d plot ? , trend line?

Question

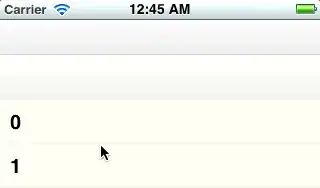
The first graph is plotted using original data, and 2nd one is drawn after applying moving average over 15 (days)

I can keep increasing the window of moving average, but it sometimes changes the overal picture.

Is there an another way of smoothing the line?

plt.plot(x,y)

def moving_avg(l, size):
    additional = int((size - 1) / 2)
    l2 = l[-additional:] + l + l[:additional]

    df = pd.DataFrame(l2, columns=["d"])

    result = (
        df.rolling(size, min_periods=size, center=True).mean()["d"].tolist()
    )
    result = result[additional:-additional]
    return result

x = range(1,365)

y = [0.25769641467531185,
 0.25769641467531185,
 0.25769641467531185,
 0.25769641467531185,
 0.15655577299412943,
 0.15655577299412943,
 0.19569471624266177,
 0.15655577299412943,
 0.19569471624266177,
 0.19569471624266177,
 0.15655577299412943,
 0.19569471624266177,
 0.19569471624266177,
 0.15655577299412943,
 0.19569471624266177,
 0.19569471624266177,
 0.19569471624266177,
 0.2968353579238442,
 0.2968353579238442,
 0.2981526713477847,
 0.31838079968402117,
 0.2792418564354889,
 0.2792418564354889,
 0.2792418564354889,
 0.21724015800283883,
 0.17810121475430643,
 0.1376449580818335,
 0.21855747142677937,
 0.21855747142677937,
 0.21855747142677937,
 0.21855747142677937,
 0.21855747142677937,
 0.25769641467531174,
 0.25769641467531174,
 0.15655577299412934,
 0.1956947162426617,
 0.25769641467531174,
 0.25769641467531174,
 0.25769641467531174,
 0.21855747142677937,
 0.25769641467531174,
 0.35883705635649416,
 0.35883705635649416,
 0.25769641467531174,
 0.25769641467531174,
 0.25769641467531174,
 0.2968353579238441,
 0.2968353579238441,
 0.234833659491194,
 0.234833659491194,
 0.33597430117237637,
 0.33597430117237637,
 0.33597430117237637,
 0.33597430117237637,
 0.33597430117237637,
 0.33597430117237637,
 0.3979759996050264,
 0.33597430117237637,
 0.33597430117237637,
 0.33597430117237637,
 0.33597430117237637,
 0.3979759996050264,
 0.3979759996050264,
 0.33597430117237637,
 0.3979759996050264,
 0.45997769803767646,
 0.4208387547891441,
 0.3816998115406118,
 0.5839810949029767,
 0.5448421516544443,
 0.6405573973141552,
 0.5899870764735639,
 0.48884643479238155,
 0.48884643479238155,
 0.5279853780409139,
 0.32570409467854905,
 0.32570409467854905,
 0.20770667938383622,
 0.19084990577030586,
 0.22998884901883823,
 0.22998884901883823,
 0.2414202266108971,
 0.3425608682920795,
 0.44370150997326185,
 0.5279853780409139,
 0.6291260197220963,
 0.6291260197220963,
 0.6682649629706285,
 0.6176946421300374,
 0.4545523020162049,
 0.3534116603350225,
 0.25227101865384016,
 0.6231200381515088,
 0.5839810949029767,
 0.6459827933356266,
 0.6459827933356266,
 0.6068438500870943,
 0.6169579142552125,
 0.6675282350958037,
 0.19553857391695253,
 0.2966792155981349,
 0.23467751716548488,
 0.28524783800607606,
 0.3243867812546084,
 0.3142727170864902,
 0.3142727170864902,
 0.3816998115406117,
 0.2805591698594293,
 0.2414202266108969,
 0.39313118913267053,
 0.39313118913267053,
 0.4942718308138529,
 0.4639296383094982,
 0.36278899662831576,
 0.3965025438553766,
 0.49764318553655895,
 0.49764318553655895,
 0.559644883969209,
 0.4585042422880266,
 0.47741505720032246,
 0.47741505720032246,
 0.4509258415219175,
 0.38349874706779596,
 0.22035640695396347,
 0.15835470852131345,
 0.1974936517698458,
 0.1974936517698458,
 0.1974936517698458,
 0.19026932022118995,
 0.15655577299412912,
 0.15655577299412912,
 0.11741682974559677,
 0.11741682974559677,
 0.0985060148333009,
 0.0985060148333009,
 0.0985060148333009,
 0.13764495808183325,
 0.0985060148333009,
 0.0985060148333009,
 0.05936707158476854,
 0.03913894324853206,
 0.0492530074166503,
 0.08839195066518266,
 0.0492530074166503,
 0.08839195066518266,
 0.12753089391371503,
 0.12753089391371503,
 0.1781012147543062,
 0.16798715058618796,
 0.12884820733765562,
 0.12884820733765562,
 0.12884820733765562,
 0.08970926408912326,
 0.12884820733765562,
 0.07827788649706442,
 0.07827788649706442,
 0.07827788649706442,
 0.1794185281782468,
 0.24142022661089685,
 0.24142022661089685,
 0.24142022661089685,
 0.24142022661089685,
 0.26670538703119245,
 0.26670538703119245,
 0.26670538703119245,
 0.20470368859854238,
 0.20470368859854238,
 0.20470368859854238,
 0.20470368859854238,
 0.22998884901883798,
 0.33112949070002035,
 0.2691277922673703,
 0.2691277922673703,
 0.2691277922673703,
 0.22998884901883798,
 0.25888617521346147,
 0.20831585437287034,
 0.14631415594022026,
 0.14631415594022026,
 0.10717521269168791,
 0.1577455335322791,
 0.25888617521346147,
 0.2906732340275474,
 0.358100328481669,
 0.358100328481669,
 0.5212426685955015,
 0.5603816118440337,
 0.5098112910034426,
 0.7120925743658073,
 0.651408189357098,
 0.6176946421300371,
 0.5785556988815047,
 0.4154133587676723,
 0.47741505720032235,
 0.5785556988815047,
 0.3004189342582532,
 0.3257040946785488,
 0.39313118913267037,
 0.39313118913267037,
 0.39313118913267037,
 0.33112949070002035,
 0.2691277922673703,
 0.3449832735282571,
 0.3196981131079615,
 0.2590137280992521,
 0.30958404893984326,
 0.3715857473724933,
 0.33244680412396094,
 0.3438781817160198,
 0.31016463448895903,
 0.33039276282519553,
 0.28993650615272254,
 0.23936618531213139,
 0.1773644868794814,
 0.1773644868794814,
 0.1659331092874225,
 0.09850601483330092,
 0.14570498095118606,
 0.3479862643135508,
 0.38712520756208313,
 0.4996972268353244,
 0.5388361700838568,
 0.4996972268353244,
 0.4996972268353244,
 0.43227013238120277,
 0.2502169773550745,
 0.21107803410654213,
 0.0985060148333009,
 0.0985060148333009,
 0.13764495808183325,
 0.13764495808183325,
 0.1767839013303656,
 0.15655577299412912,
 0.15655577299412912,
 0.15655577299412912,
 0.15655577299412912,
 0.11741682974559677,
 0.21855747142677917,
 0.3816998115406116,
 0.42083875478914395,
 0.4599776980376763,
 0.4599776980376763,
 0.4599776980376763,
 0.49911664128620864,
 0.3979759996050262,
 0.2534893686319086,
 0.3154910670645586,
 0.3154910670645586,
 0.3154910670645586,
 0.27635212381602625,
 0.23721318056749394,
 0.23721318056749394,
 0.17941852817824683,
 0.07827788649706446,
 0.03913894324853211,
 0.20228128336236453,
 0.20228128336236453,
 0.20228128336236453,
 0.20228128336236453,
 0.24142022661089685,
 0.3931311891326704,
 0.43227013238120277,
 0.2691277922673704,
 0.3082667355159027,
 0.34740567876443507,
 0.3865446220129674,
 0.6508276038079822,
 0.49911664128620864,
 0.4599776980376763,
 0.42083875478914395,
 0.4154133587676724,
 0.40998796274620086,
 0.3708490194976685,
 0.08187575755143311,
 0.09030414435819832,
 0.12944308760673068,
 0.12944308760673068,
 0.13486848362820222,
 0.10115493640114144,
 0.11560359949845322,
 0.12644009682143703,
 0.1571506532632042,
 0.11801171001467185,
 0.11801171001467185,
 0.11801171001467185,
 0.1571506532632042,
 0.19327231100648368,
 0.26912779226737044,
 0.2637023962458989,
 0.30284133949443126,
 0.30284133949443126,
 0.30284133949443126,
 0.2974159434729597,
 0.2859845658809008,
 0.18484392419971843,
 0.17135850530889415,
 0.1322195620603618,
 0.17135850530889415,
 0.1322195620603618,
 0.13764495808183336,
 0.1996466565144834,
 0.1996466565144834,
 0.2299888490188381,
 0.2691277922673704,
 0.2299888490188381,
 0.2691277922673704,
 0.2691277922673704,
 0.20844340725866098,
 0.24758235050719332,
 0.19701202966660214,
 0.1970120296666021,
 0.2361509729151345,
 0.1970120296666021,
 0.1970120296666021,
 0.19569471624266155,
 0.19026932022118997,
 0.2155544806414856,
 0.17641553739295326,
 0.1372765941444209,
 0.17641553739295326,
 0.17641553739295326,
 0.1372765941444209,
 0.14270199016589247,
 0.1565557729941292,
 0.19569471624266158,
 0.2348336594911939,
 0.19569471624266158,
 0.1565557729941292,
 0.19569471624266158,
 0.19026932022118997,
 0.15113037697265763,
 0.11199143372412527,
 0.11199143372412527,
 0.15113037697265763,
 0.15113037697265763,
 0.15113037697265763,
 0.16798715058618804,
 0.20712609383472042,
 0.24626503708325276,
 0.24626503708325276,
 0.24626503708325276,
 0.24626503708325276,
 0.24626503708325276,
 0.2348336594911939,
 0.2348336594911939,
 0.2348336594911939,
 0.2348336594911939,
 0.2348336594911939,
 0.27397260273972623,
 0.27397260273972623,
 0.2348336594911939,
 0.2348336594911939,
 0.2348336594911939,
 0.19569471624266158,
 0.19569471624266158,
 0.19569471624266158,
 0.1565557729941292,
 0.1565557729941292,
 0.11741682974559685,
 0.11741682974559685,
 0.1565557729941292,
 0.21855747142677923,
 0.21855747142677923,
 0.21855747142677923]

The following shows

sns.distplot(y, bins=100, color='k')

(ok it's a different plot)

But it's also very stepwise and somehow seaborn manages to draw smooth line over it..

How does it do it?

Practically, the following is the best I have now

y_new = moving_avg(y, 31)
import numpy as np
import matplotlib.pyplot as plt

from csaps import csaps

np.random.seed(1234)

xs = np.linspace(x[0], x[-1], 52)

ys = csaps(x, y_new, xs, smooth=0.85)

plt.plot(x, y, 'o', xs, ys, '-')

Your data is very stepwise. I'm not sure it's realistic to expect a smooth result. There are a very large number of smoothing algorithms. Butterworth filters do a nice job. Exponential smoothing is similar to a running average but softens the edges. https://en.wikipedia.org/wiki/Smoothing — Tim Roberts, Feb 04 '21 at 07:42
the following thread might be helpful: [python-natural-smoothing-splines](https://stackoverflow.com/questions/51321100/python-natural-smoothing-splines) — Marc, Feb 04 '21 at 07:50
@Marc indeed https://stackoverflow.com/a/55481248/433570 I could use it.. thanks — eugene, Feb 04 '21 at 08:17
Regarding how seaborn does it for histograms: [kernel density estimation](https://seaborn.pydata.org/tutorial/distributions.html#kernel-density-estimation). — Patrick FitzGerald, Feb 08 '21 at 19:48

score 1 · Accepted Answer · answered Feb 04 '21 at 12:58

I was taught the following technique at uni for finding the trendline in biosignals (ppg, ecg, etc), by firstly applying a moving mean to the signal and then a Savitzky-Golay Smoothing Filter

The code is below, I have used another moving average technique which i get along with more from here: How to calculate rolling / moving average using NumPy / SciPy?

and the Savitzky-Golay filter from Scipy: https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.savgol_filter.html

import numpy as np
from scipy.signal import savgol_filter

y = np.array(y)
x = range(1,365)

## from: https://stackoverflow.com/questions/14313510/how-to-calculate-rolling-moving-average-using-numpy-scipy
def moving_average(x, w):
    return np.convolve(x, np.ones(w), 'valid') / w

y_ave = moving_average(y, 10)  ## moving average
x_ave = np.arange(x[0], x[-1], x[-1]/y_ave.shape[0]) ## compensate for shorter signal 
y_savgol = savgol_filter(y_ave, 99, 3) ## Savitzky-Golay filtering 

fig, axs = plt.subplots(1, figsize=(30,15))
axs.plot(x,y)
axs.plot(x_ave,y_savgol)
print(y_savgol.shape)

you can use the documentation above to adjust the parameters in order to achieve the results you are looking for, the code was able to produce the following figure - which may be too much smoothing depending on what you want to achieve:

wow.. splendid .. must be very good univ.. ! – eugene Feb 05 '21 at 05:13 — eugene, Feb 05 '21 at 05:13
glad I could offer something useful – Maxwell Redacted Feb 05 '21 at 21:04 — Maxwell Redacted, Feb 05 '21 at 21:04

python, smoothing 2d plot ? , trend line?

1 Answers1