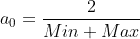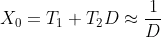The ISO-C99 code below demonstrates how one can achieve an almost correctly rounded implementation of Newton-Raphson based s15.16 division, using a 2 kilobit lookup table for the initial reciprocal approximation, and a number of 32x32-bit multipliers capable of delivering both the low 32 bits of the full product and the high 32 bits. For ease of implementation the signed s15.16 division is mapped back to unsigned 16.16 division for operands in [0, 231].
We need to make full use of the 32-bit data path throughout by keeping operands normalized. In essence we are converting the computation into a quasi floating-point format. This requires a priority encoder to find the most significant set bit in both the dividend and the divisor in the initial normalization step. For software convenience, this is mapped to a CLZ (count leading zeros) operation, present in many processors, in the code below.
After computing the reciprocal of the divisor b we multiply by the dividend a to determine the raw quotient q = (1/b)*a. In order to round correctly to nearest or even we need to compute the remainder for the quotient a well as its increment and decrement. The correctly rounded quotient corresponds to the candidate quotient with the remainder of smallest magnitude.
In order for this to work perfectly, we would need a raw quotient that is within 1 ulp of the mathematical result. Unfortunately, this is not the case here, since the raw quotient is occasionally off by ±2 ulps. We would need effectively 33 bits in some of the intermediate computation, which could be simulated in software but I don't have time to puzzle this out right now. The code "as-is" delivers the correctly rounded result in more than 99.999% of random test cases.
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
#define TAB_BITS_IN (8) /* 256 entry LUT */
#define TAB_BITS_OUT (9) /* 9 bits effective, 8 bits stored */
#define TRUNC_COMP (1) /* compensate truncation in fixed-point multiply */
int clz (uint32_t a); // count leadzing zeros: a priority encoder
uint32_t umul32_hi (uint32_t a, uint32_t b); // upper half of 32x32-bit product
/* i in [0,255]: (int)(1.0 / (1.0 + 1.0/512.0 + i / 256.0) * 512 + .5) & 0xff
In a second step tuned to minimize the number of incorrect results with the
specific implementation of the two refinement steps chosen.
*/
static uint8_t rcp_tab[256] =
{
0xff, 0xfd, 0xfb, 0xf9, 0xf7, 0xf5, 0xf3, 0xf1,
0xf0, 0xee, 0xec, 0xea, 0xe8, 0xe6, 0xe5, 0xe3,
0xe1, 0xdf, 0xdd, 0xdc, 0xda, 0xd8, 0xd7, 0xd5,
0xd3, 0xd2, 0xd0, 0xce, 0xcd, 0xcb, 0xc9, 0xc8,
0xc6, 0xc5, 0xc3, 0xc2, 0xc0, 0xbf, 0xbd, 0xbc,
0xba, 0xb9, 0xb7, 0xb6, 0xb4, 0xb3, 0xb1, 0xb0,
0xae, 0xad, 0xac, 0xaa, 0xa9, 0xa7, 0xa6, 0xa5,
0xa4, 0xa2, 0xa1, 0x9f, 0x9e, 0x9d, 0x9c, 0x9a,
0x99, 0x98, 0x96, 0x95, 0x94, 0x93, 0x91, 0x90,
0x8f, 0x8e, 0x8c, 0x8b, 0x8a, 0x89, 0x88, 0x87,
0x86, 0x84, 0x83, 0x82, 0x81, 0x80, 0x7f, 0x7e,
0x7c, 0x7b, 0x7a, 0x79, 0x78, 0x77, 0x76, 0x74,
0x74, 0x73, 0x71, 0x71, 0x70, 0x6f, 0x6e, 0x6d,
0x6b, 0x6b, 0x6a, 0x68, 0x67, 0x67, 0x66, 0x65,
0x64, 0x63, 0x62, 0x61, 0x60, 0x5f, 0x5e, 0x5d,
0x5c, 0x5b, 0x5b, 0x59, 0x58, 0x58, 0x56, 0x56,
0x55, 0x54, 0x53, 0x52, 0x51, 0x51, 0x50, 0x4f,
0x4e, 0x4e, 0x4c, 0x4b, 0x4b, 0x4a, 0x48, 0x48,
0x48, 0x46, 0x46, 0x45, 0x44, 0x43, 0x43, 0x42,
0x41, 0x40, 0x3f, 0x3f, 0x3e, 0x3d, 0x3c, 0x3b,
0x3b, 0x3a, 0x39, 0x38, 0x38, 0x37, 0x36, 0x36,
0x35, 0x34, 0x34, 0x33, 0x32, 0x31, 0x30, 0x30,
0x2f, 0x2e, 0x2e, 0x2d, 0x2d, 0x2c, 0x2b, 0x2a,
0x2a, 0x29, 0x28, 0x27, 0x27, 0x26, 0x26, 0x25,
0x24, 0x23, 0x23, 0x22, 0x21, 0x21, 0x21, 0x20,
0x1f, 0x1f, 0x1e, 0x1d, 0x1d, 0x1c, 0x1c, 0x1b,
0x1a, 0x19, 0x19, 0x19, 0x18, 0x17, 0x17, 0x16,
0x16, 0x15, 0x14, 0x13, 0x13, 0x12, 0x12, 0x11,
0x11, 0x10, 0x0f, 0x0f, 0x0e, 0x0e, 0x0e, 0x0d,
0x0c, 0x0c, 0x0b, 0x0b, 0x0a, 0x0a, 0x09, 0x08,
0x08, 0x07, 0x07, 0x07, 0x06, 0x05, 0x05, 0x04,
0x04, 0x03, 0x03, 0x02, 0x02, 0x01, 0x01, 0x01
};
/* Divide two u16.16 fixed-point operands each in [0, 2**31]. Attempt to round
the result to nearest of even. Currently this does not always succeed. We
would need effectively 33 bits in intermediate computation for that, so the
raw quotient is within +/- 1 ulp of the mathematical result.
*/
uint32_t div_core (uint32_t a, uint32_t b)
{
/* normalize dividend and divisor to [1,2); bit 31 is the integer bit */
uint8_t lza = clz (a);
uint8_t lzb = clz (b);
uint32_t na = a << lza;
uint32_t nb = b << lzb;
/* LUT is addressed by most significant fraction bits of divisor */
uint32_t idx = (nb >> (32 - 1 - TAB_BITS_IN)) & 0xff;
uint32_t rcp = rcp_tab [idx] | 0x100; // add implicit msb
/* first NR iteration */
uint32_t f = (rcp * rcp) << (32 - 2*TAB_BITS_OUT);
uint32_t p = umul32_hi (f, nb);
rcp = (rcp << (32 - TAB_BITS_OUT)) - p;
/* second NR iteration */
rcp = rcp << 1;
p = umul32_hi (rcp, nb);
rcp = umul32_hi (rcp, 0 - p);
/* compute raw quotient as (1/b)*a; off by at most +/- 2ulps */
rcp = (rcp << 1) | TRUNC_COMP;
uint32_t quot = umul32_hi (rcp, na);
uint8_t shift = lza - lzb + 15;
quot = (shift > 31) ? 0 : (quot >> shift);
/* round quotient using 4:1 mux */
uint32_t ah = a << 16;
uint32_t prod = quot * b;
uint32_t rem1 = abs (ah - prod);
uint32_t rem2 = abs (ah - prod - b);
uint32_t rem3 = abs (ah - prod + b);
int sel = (((rem2 < rem1) << 1) | ((rem3 < rem1) & (quot != 0)));
switch (sel) {
case 0:
default:
quot = quot;
break;
case 1:
quot = quot - 1;
break;
case 2: /* fall through */
case 3:
quot = quot + 1;
break;
}
return quot;
}
int32_t div_s15p16 (int32_t a, int32_t b)
{
uint32_t aa = abs (a);
uint32_t ab = abs (b);
uint32_t quot = div_core (aa, ab);
quot = ((a ^ b) & 0x80000000) ? (0 - quot) : quot;
return (int32_t)quot;
}
uint64_t umul32_wide (uint32_t a, uint32_t b)
{
return ((uint64_t)a) * b;
}
uint32_t umul32_hi (uint32_t a, uint32_t b)
{
return (uint32_t)(umul32_wide (a, b) >> 32);
}
#define VARIANT (1)
int clz (uint32_t a)
{
#if VARIANT == 1
static const uint8_t clz_tab[32] = {
31, 22, 30, 21, 18, 10, 29, 2, 20, 17, 15, 13, 9, 6, 28, 1,
23, 19, 11, 3, 16, 14, 7, 24, 12, 4, 8, 25, 5, 26, 27, 0
};
a |= a >> 16;
a |= a >> 8;
a |= a >> 4;
a |= a >> 2;
a |= a >> 1;
return clz_tab [0x07c4acddu * a >> 27] + (!a);
#elif VARIANT == 2
uint32_t b;
int n = 31 + (!a);
if ((b = (a & 0xffff0000u))) { n -= 16; a = b; }
if ((b = (a & 0xff00ff00u))) { n -= 8; a = b; }
if ((b = (a & 0xf0f0f0f0u))) { n -= 4; a = b; }
if ((b = (a & 0xccccccccu))) { n -= 2; a = b; }
if (( (a & 0xaaaaaaaau))) { n -= 1; }
return n;
#elif VARIANT == 3
int n = 0;
if (!(a & 0xffff0000u)) { n |= 16; a <<= 16; }
if (!(a & 0xff000000u)) { n |= 8; a <<= 8; }
if (!(a & 0xf0000000u)) { n |= 4; a <<= 4; }
if (!(a & 0xc0000000u)) { n |= 2; a <<= 2; }
if ((int32_t)a >= 0) n++;
if ((int32_t)a == 0) n++;
return n;
#elif VARIANT == 4
uint32_t b;
int n = 32;
if ((b = (a >> 16))) { n = n - 16; a = b; }
if ((b = (a >> 8))) { n = n - 8; a = b; }
if ((b = (a >> 4))) { n = n - 4; a = b; }
if ((b = (a >> 2))) { n = n - 2; a = b; }
if ((b = (a >> 1))) return n - 2;
return n - a;
#endif
}
uint32_t div_core_ref (uint32_t a, uint32_t b)
{
int64_t quot = ((int64_t)a << 16) / b;
/* round to nearest or even */
int64_t rem1 = ((int64_t)a << 16) - quot * b;
int64_t rem2 = rem1 - b;
if (llabs (rem2) < llabs (rem1)) quot++;
if ((llabs (rem2) == llabs (rem1)) && (quot & 1)) quot &= ~1;
return (uint32_t)quot;
}
// George Marsaglia's KISS PRNG, period 2**123. Newsgroup sci.math, 21 Jan 1999
// Bug fix: Greg Rose, "KISS: A Bit Too Simple" http://eprint.iacr.org/2011/007
static uint32_t kiss_z=362436069, kiss_w=521288629;
static uint32_t kiss_jsr=123456789, kiss_jcong=380116160;
#define znew (kiss_z=36969*(kiss_z&65535)+(kiss_z>>16))
#define wnew (kiss_w=18000*(kiss_w&65535)+(kiss_w>>16))
#define MWC ((znew<<16)+wnew )
#define SHR3 (kiss_jsr^=(kiss_jsr<<13),kiss_jsr^=(kiss_jsr>>17), \
kiss_jsr^=(kiss_jsr<<5))
#define CONG (kiss_jcong=69069*kiss_jcong+1234567)
#define KISS ((MWC^CONG)+SHR3)
int main (void)
{
uint64_t count = 0ULL, stats[3] = {0ULL, 0ULL, 0ULL};
uint32_t a, b, res, ref;
do {
/* random dividend and divisor, avoiding overflow and divison by zero */
do {
a = KISS % 0x80000001u;
b = KISS % 0x80000001u;
} while ((b == 0) || ((((uint64_t)a << 16) / b) > 0x80000000ULL));
/* compute function under test and reference result */
ref = div_core_ref (a, b);
res = div_core (a, b);
if (llabs ((int64_t)res - (int64_t)ref) > 1) {
printf ("\nerror: a=%08x b=%08x res=%08x ref=%08x\n", a, b, res, ref);
break;
} else {
stats[(int64_t)res - (int64_t)ref + 1]++;
}
count++;
if (!(count & 0xffffff)) {
printf ("\r[-1]=%llu [0]=%llu [+1]=%llu", stats[0], stats[1], stats[2]);
}
} while (count);
return EXIT_SUCCESS;
}