All the testcases for this code is not passing. Can you say me how can I obtain it?

Question

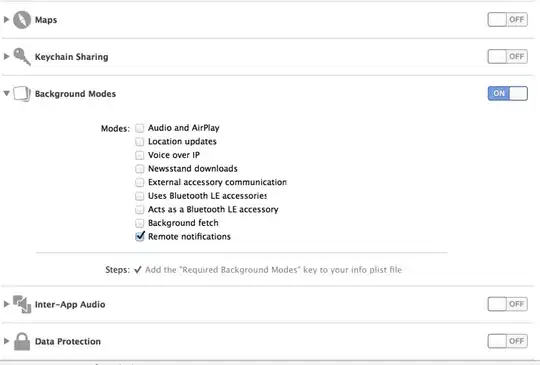
Question:
A circle of radius R cm is touching both the positive axes i.e., the X-axis and the Y-axis. There is another circle touching both the axes as well as the previous circle. Note that this circle won't have the same center as the original circle. The question is to find the sum of squares of the radius of all the circles that satisfies the condition.

#include <stdio.h>
#include <math.h>

int roundNo(double num) 
{ 
    return (int)(num + 0.5);
} 
    
int main()
{
    double multiplier1 = 2*sqrt(2) + 3;
    double multiplier2 = 1/multiplier1;
    int t;

    scanf("%d",&t);

    for (int i = 0; i < t; i++) {
        double sum;
        int n;
            
        scanf("%d", &n);
        sum = (2 + pow(multiplier1, 2) + pow(multiplier2, 2))*pow(n, 2);
            
        printf("%d\n", roundNo(sum));
    }
}

We have to print the integer sum for the test cases. So I have rounded them off.

Answer 1

I think that your problem is like below:

This is the math problem, not the programming.

Now there are two ways. One approach is

#include <stdio.h>
#include <math.h>

const double multiplier = 1.030330085889911;

int round(double num)
{
    return (int)(num + 0.5);
}

int main()
{
    int R0;
    printf("Input R0: ");
    scanf("%d", &R0);

    double S = pow((double)R0, 2) / (sqrt(2.0) * 12 - 16);
    printf("S = %d\n", round(S));

    return 0;
}

The other is more programmatically

#include <stdio.h>
#include <math.h>

const double threshold = 0.001;

int round(double num)
{
    return (int)(num + 0.5);
}

int main()
{
    int R0;
    printf("Input R0: ");
    scanf("%d", &R0);
    
    int i = 0;
    double Ri = R0;
    double S = R0 * R0;

    while (Ri > threshold)
    {
        i++;
        Ri = (3.0 - 2.0 * sqrt(2.0)) * Ri;

        S+= (Ri * Ri);
    }

    printf("i: %d, Ri: %f, S = %d\n", i, Ri, round(S));
    return 0;
}

Answer 2

While this is just a tricky math problem, there are many issues in the posted implementation.

The formula is (analitically) correct, if we consider all the four circles touching both the axes as well as the original circle:

The posted code failed to perform some fundamental simplifications, though.

• The requested sum is obtained by multipling the square of the inputted radius times a constant, indipendent from said radius. While an optimizing compiler might be smart enough not to repeat all theese calculations, it would be better (at least for documentation purposes) to explicitly calculate this multiplier once and store its value in a const or constexpr variable.

• The value of this multiplier is exactly 36 (the test case already told us), so there's no need to use a double nor to round floating point values:

The main issue, however, is a pure coding bug.

One of the constraints of the problem (from OP's comments) is 1 ≤ R ≤ 10^8, but the result is returned by roundNo as int, which isn't required to be a 64-bit wide type.

It's more than likely that some test cases had a value of the radius big enough to produce a sum bigger than the maximum value storable in an int, introducing undefined behaviour.

The following should work for all the test cases.

long long sum = 36LL * radius * radius;

Note that, thanks to the integer literal and its LL suffix, even if radius was an int (or a long, to be sure), it would be converted to a long long before beeing multiplied by itself. Also, there's no need to use pow and deal with floating-point types.